
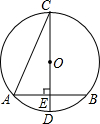
 如圖,⊙O的直徑CD垂直于弦AB,垂足為E,∠ACD=22.5°,CD=4.
如圖,⊙O的直徑CD垂直于弦AB,垂足為E,∠ACD=22.5°,CD=4.分析 (1)根據(jù)等邊對等角可得∠OAC=∠OCA=22.5°,再根據(jù)三角形外角的性質(zhì)可得∠COE=45°,進而求出AE的長,再根據(jù)垂徑定理可得答案;
(2)求出CE的長,利用正切值的定義求出答案.
解答 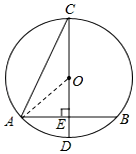 解:(1)連結(jié)OA.
解:(1)連結(jié)OA.
∵∠ACD=22.5°,
∴∠AOD=45°,
∵CD⊥AB,
∴∠AEO=90°,
∴AE=OE,
在Rt△AOE中,OA=2,
∴AE=OE=$\sqrt{2}$,
由垂徑定理,得AB=2AE=2$\sqrt{2}$;
(2)∵CE=2+$\sqrt{2}$,AE=$\sqrt{2}$,
∴tan∠BAC=$\frac{CE}{AE}$=$\frac{2+\sqrt{2}}{\sqrt{2}}$=$\sqrt{2}$+1.
點評 此題主要考查了圓周角定理、垂徑定理以及解直角三角形等知識,關(guān)鍵是掌握垂直弦的直徑平分這條弦,并且平分弦所對的兩條弧.


 期末集結(jié)號系列答案
期末集結(jié)號系列答案科目:初中數(shù)學 來源: 題型:解答題
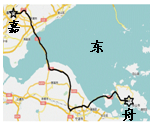 國慶期間,林老師駕轎車從舟山出發(fā),上高速途經(jīng)舟山跨海大橋和杭州灣跨海大橋到嘉興下高速,其間用了4.5小時;返回時平均速度提高了10千米/小時,比去時少用了半小時回到舟山.
國慶期間,林老師駕轎車從舟山出發(fā),上高速途經(jīng)舟山跨海大橋和杭州灣跨海大橋到嘉興下高速,其間用了4.5小時;返回時平均速度提高了10千米/小時,比去時少用了半小時回到舟山.| 大橋名稱 | 舟山跨海大橋 | 杭州灣跨海大橋 |
| 大橋長度 | 48千米 | 36千米 |
| 過橋費 | 100元 | 80元 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
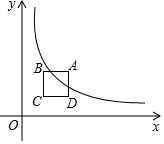 如圖,在平面直角坐標系的第一象限內(nèi),邊長為1的正方形ABCD的邊均平行于坐標軸,A點的坐標為(a,a),若雙曲線y=$\frac{4}{x}$(x>0)與此正方形的邊有交點.
如圖,在平面直角坐標系的第一象限內(nèi),邊長為1的正方形ABCD的邊均平行于坐標軸,A點的坐標為(a,a),若雙曲線y=$\frac{4}{x}$(x>0)與此正方形的邊有交點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 5,12,13 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,12 | D. | 3a,4a,5a(a>0) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 66πcm2 | B. | 15πcm2 | C. | 28πcm2 | D. | 30πcm2 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com