
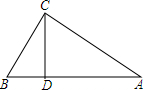
 如圖,D為△ABC邊AB上一點,且CD分△ABC為兩個相似比為1:$\sqrt{3}$的一對相似三角形;(不妨如圖假設左小右大),求:
如圖,D為△ABC邊AB上一點,且CD分△ABC為兩個相似比為1:$\sqrt{3}$的一對相似三角形;(不妨如圖假設左小右大),求:分析 (1)根據相似三角形面積的比等于相似比的平方解答;
(2)根據銳角三角函數的概念解答即可.
解答 解:(1)∵△BCD和△CAD的相似比為1:$\sqrt{3}$,
∴△BCD和△CAD的面積比為1:3;
(2)∵△BCD∽△CAD,
∴∠BDC=∠ADC=90°,
tanA=$\frac{CD}{AD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
tanB=$\frac{CD}{BD}$=$\sqrt{3}$,
∴∠B=60°,
∴∠ACB=90°.
點評 本題考查的是相似三角形的性質,掌握相似三角形面積的比等于相似比的平方以及銳角三角函數的概念是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 李先生準備在永川某小區內購買一套小戶型商品房,他去某樓盤了解情況得知,該戶型商品房的單價是8000元/m2,面積如圖所示(單位:m,衛生間的寬未定,設寬為xm),售房部為李先生提供了以下兩種優惠方案:
李先生準備在永川某小區內購買一套小戶型商品房,他去某樓盤了解情況得知,該戶型商品房的單價是8000元/m2,面積如圖所示(單位:m,衛生間的寬未定,設寬為xm),售房部為李先生提供了以下兩種優惠方案:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
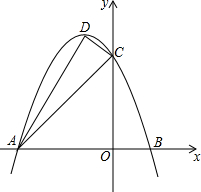 如圖拋物線y=ax2+bx+3與x軸交于A(-3,0),B(1,0)兩點,與y軸交于點C,頂點為D,連接AC、CD、AD.
如圖拋物線y=ax2+bx+3與x軸交于A(-3,0),B(1,0)兩點,與y軸交于點C,頂點為D,連接AC、CD、AD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -5 | B. | 2 | C. | 1 | D. | 7 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省連云港市灌云縣西片九年級下學期第一次月考數學試卷(解析版) 題型:填空題
如圖,小明同學測量一個光盤的直徑,他只有一把直尺和一塊三角板,他將直尺、光盤和三角板如圖放置于桌面上,并量出AB=3cm,則此光盤的直徑是__cm.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com