
分析 分兩種情況:
解法一:①當E在BA的延長線上時,如圖1,作輔助線,構建直角三角形,先根據勾股定理列等式求AH的長,從而繼續求CH、BH的長,從而可以求EC的長,設FN=a,則EN=2a,可求FN=$\frac{2\sqrt{5}}{5}$,EN=$\frac{4\sqrt{5}}{5}$,由此求EF的長,得出AF的長;
②當E在線段AB上時,如圖2,同樣的方法可求得AF的長.
解法二,兩種情況都設某一個角為x°,分別表示其它角,利用等角對等邊,得出線段的長,計算AF的長.
解答 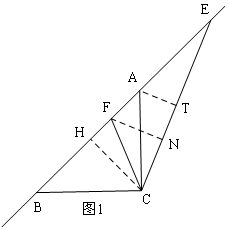 解法一:分兩種情況:
解法一:分兩種情況:
①當E在BA的延長線上時,如圖1,
過C作CH⊥AB于H,
設AH=x,則BH=2.5-x,
由勾股定理得:CH2=AC2-AH2=1.52-x2,
CH2=BC2-BH2=22-(2.5-x)2,
∴1.52-x2=22-(2.5-x)2,
x=0.9,
∴AH=0.9,
∴HE=AH+AE=0.9+1.5=2.4,
CH=$\sqrt{A{C}^{2}-A{H}^{2}}$=$\sqrt{1.{5}^{2}-0.{9}^{2}}$=1.2,
在Rt△ECH中,EC=$\sqrt{C{H}^{2}+H{E}^{2}}$=$\sqrt{1.{2}^{2}+2.{4}^{2}}$=$\frac{6\sqrt{5}}{5}$,
過F作FN⊥EC于N,過A作AT⊥EC于T,
由tan∠E=$\frac{CH}{EH}=\frac{FN}{EN}=\frac{1.2}{2.4}=\frac{1}{2}$,
設FN=a,則EN=2a,
∵∠ECF=45°,
∴△FCN是等腰直角三角形,
∴FN=NC=a,
∴EC=EN+CN=2a+a=$\frac{6\sqrt{5}}{5}$,
a=$\frac{2\sqrt{5}}{5}$,
在△EFN中,FN=$\frac{2\sqrt{5}}{5}$,EN=$\frac{4\sqrt{5}}{5}$,
∴EF=$\sqrt{F{N}^{2}+E{N}^{2}}$=2,
∴AF=EF-AE=2-1.5=0.5;
②當E在線段AB上時,如圖2,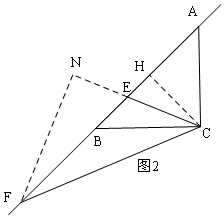
過C作CH⊥AB于H,
同理得:AH=0.9,CH=1.2,
∵AC=AE=1.5,
∴EH=AE-AH=1.5-0.9=0.6,
由勾股定理得:CE=$\sqrt{1.{2}^{2}-0.{6}^{2}}$=$\frac{3\sqrt{5}}{5}$,
∴tan∠ECH=$\frac{EH}{CH}=\frac{1}{2}$,
過F作FN⊥EC于N,
∵∠ECF=45°,
∴△FCN是等腰直角三角形,
∴FN=CN,
∵∠FNC=∠EHC=90°,
∠NEF=∠HEC,
∴∠NFE=∠ECH,
∴tan∠NFE=$\frac{EN}{FN}=\frac{1}{2}$,
∴FN=CN=2EN,
∴CE=EN=$\frac{3\sqrt{5}}{5}$,
由勾股定理得:EF=$\sqrt{F{N}^{2}+E{N}^{2}}$=$\sqrt{(\frac{6\sqrt{5}}{5})^{2}+(\frac{3\sqrt{5}}{5})^{2}}$=3,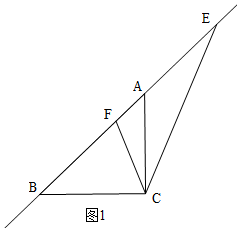
∴AF=AE+EF=1.5+3=4.5,
綜上所述,AF的長為0.5或4.5;
解法二:分兩種情況:
①當E在BA的延長線上時,如右圖1,
設∠E=x°,則∠ACE=x°,∠ACF=45°-x°,
∵∠ACB=90°,
∴∠BCF=90°-(45°-x°)=45°+x°,
∵∠CFB=∠E+∠ECF=45°+x°,
∴∠BCF=∠CFB,
∴BC=BF=2,
∴AF=AB-BF=2.5-2=0.5;
②當E在線段AB上時,如右圖2,
設∠AEC=x°,則∠ACE=x°,
∴∠BCE=90°-x°,
∴∠BCF=∠ECF-∠BCE=45°-(90°-x°)=x°-45°,
∵∠F=x°-45°,
∴∠F=∠BCF,
∴BC=BF=2,
∴AF=AB+BF=2.5+2=4.5,
故答案為:0.5或4.5.
點評 本題考查了勾股定理、等腰直角三角形的性質和判定、同角的三角函數,熟練掌握勾股定理列方程是關鍵,恰當地作輔助線是本題的突破口,有難度,同時要注意“E、F均在直線AB上”,根據數形結合采用分類討論的思想解決問題.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:解答題
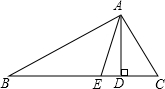 如圖,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分線,AD是高.
如圖,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分線,AD是高.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com