
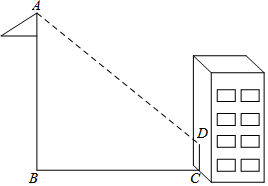
 數學興趣小組的同學們,想利用自己所學的數學知識測量學校旗桿的高度:下午活動時間,興趣小組的同學們來到操場,發現旗桿的影子有一部分落在了墻上(如圖所示).同學們按照以下步驟進行測量:測得小明的身高1.65米,此時其影長為2.5米;在同一時刻測量旗桿影子落在地面上的影長BC為9米,留在墻上的影高CD為2米,請你幫助興趣小組的同學們計算旗桿的高度.
數學興趣小組的同學們,想利用自己所學的數學知識測量學校旗桿的高度:下午活動時間,興趣小組的同學們來到操場,發現旗桿的影子有一部分落在了墻上(如圖所示).同學們按照以下步驟進行測量:測得小明的身高1.65米,此時其影長為2.5米;在同一時刻測量旗桿影子落在地面上的影長BC為9米,留在墻上的影高CD為2米,請你幫助興趣小組的同學們計算旗桿的高度. 分析 作DH⊥AB于H,如圖,利用四邊形BCDH為矩形得到BH=CD=2,DH=BC=9,再根據在同一時刻物高與影長的比相等$\frac{AH}{DH}$=$\frac{1.65}{2.5}$,則可計算出AH,然后計算AH+BH即可得到旗桿的高度.
解答 解:作DH⊥AB于H,如圖,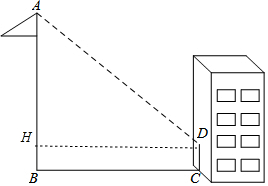
易得四邊形BCDH為矩形,
∴BH=CD=2,DH=BC=9,
∵小明的身高1.65米,此時其影長為2.5米,
∴$\frac{AH}{DH}$=$\frac{1.65}{2.5}$,
∴AH=$\frac{1.65×9}{2.5}$=5.95,
∴AB=AH+BH=5.95+2=7.95.
答:旗桿的高度為7.95m.
點評 本題考查了相似三角形的應用:利用影長測量物體的高度,通常利用相似三角形的性質即相似三角形的對應邊的比相等和“在同一時刻物高與影長的比相等”的原理解決.


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數學 來源: 題型:選擇題
 如圖,⊙O的直徑AB垂直于弦CD,垂足是E,∠A=30°,AB=4$\sqrt{3}$,則CD的長為( )
如圖,⊙O的直徑AB垂直于弦CD,垂足是E,∠A=30°,AB=4$\sqrt{3}$,則CD的長為( )| A. | 2$\sqrt{3}$ | B. | 6 | C. | 4$\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
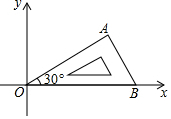 將含有30°角的直角三角板OAB如圖放置在平面直角坐標中,OB在x軸上,若OA=2,將三角板繞原點O順時針旋轉75°,則點A的對應點A′的坐標為( )
將含有30°角的直角三角板OAB如圖放置在平面直角坐標中,OB在x軸上,若OA=2,將三角板繞原點O順時針旋轉75°,則點A的對應點A′的坐標為( )| A. | ($\sqrt{3}$,1) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
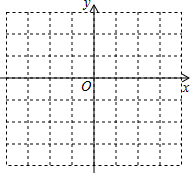 如圖,△ABC的三個頂點在邊長為1的正方形網格中,已知A(-1,-1),B(4,-1),C(3,1).
如圖,△ABC的三個頂點在邊長為1的正方形網格中,已知A(-1,-1),B(4,-1),C(3,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 兩個陌生人甲、乙同在如圖所示的地下車庫等電梯,已知兩個陌生人到1至4層的任意一層出電梯.
兩個陌生人甲、乙同在如圖所示的地下車庫等電梯,已知兩個陌生人到1至4層的任意一層出電梯.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com