
【題目】點![]() 在直線
在直線![]() 上,已知點
上,已知點![]() 是
是![]() 的中點,點
的中點,點![]() 是
是![]() 的中點,AB=6cm,BC=4cm,求
的中點,AB=6cm,BC=4cm,求![]() 的長. (要求考慮可能出現(xiàn)的情況,畫出圖形,寫出完整解答過程)
的長. (要求考慮可能出現(xiàn)的情況,畫出圖形,寫出完整解答過程)
【答案】1cm或5cm
【解析】
根據(jù)題意分兩種情況,畫出圖形,第一種情況是點C在線段AB之間時,此時MN的之間的距離為BM與BN之差;第二種情況是點C在線段AB的延長線上,此時MN的之間的距離為BM與BN之和.
解:①如圖所示,當(dāng)點C在線段AB之間時,
![]()
AB=6cm,BC=4cm
則AM=BM=![]() AB=3cm,BN=CN=
AB=3cm,BN=CN=![]() BC=2cm,
BC=2cm,
∴MN=BM-BN=3-2=1cm;
②如圖所示,當(dāng)點C在線段AB之外時,
![]()
AB=6cm,BC=4cm,
則AM=BM=![]() AB=3cm,BN=CN=
AB=3cm,BN=CN=![]() BC=2cm,
BC=2cm,
∴MN=BM+BN=3+2=5cm
綜上所述,MN的長為1cm或5cm.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一次函數(shù)y=kx+b在y軸上的截距為4且與兩坐標(biāo)軸圍成的三角形面積為4,則此一次函數(shù)解析式為________________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
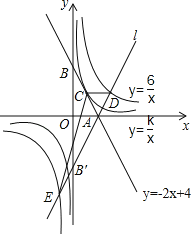
【題目】如圖,直線y=﹣2x+4交x軸于點A,交y軸于點B,與反比例函數(shù)y=![]() 的圖象有唯一的公共點C.
的圖象有唯一的公共點C.
(1)求k的值及C點坐標(biāo);
(2)直線l與直線y=﹣2x+4關(guān)于x軸對稱,且與y軸交于點B',與雙曲線y=![]() 交于D、E兩點,求△CDE的面積.
交于D、E兩點,求△CDE的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
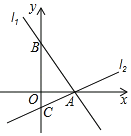
【題目】如圖,過點A(4,0)的兩條直線l1,l2分別交y軸于點B,C,其中點B在原點上方,點C在原點下方,已知AB=2![]() .
.
(1)求點B的坐標(biāo);
(2)若△ABC的面積為20,求直線l2的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“歡樂跑中國重慶站”比賽前夕,小剛和小強(qiáng)相約晨練跑步.小剛比小強(qiáng)早1分鐘跑步出門,3分鐘后他們相遇.兩人寒暄2分鐘后,決定進(jìn)行跑步比賽.比賽時小剛的速度始終是180米/分,小強(qiáng)的速度是220米/分.比賽開始10分鐘后,因霧霾嚴(yán)重,小強(qiáng)突感身體不適,于是他按原路以出門時的速度返回,直到他們再次相遇.如圖所示是小剛、小強(qiáng)之間的距離y(千米)與小剛跑步所用時間x(分鐘)之間的函數(shù)圖象.問小剛從家出發(fā)到他們再次相遇時,一共用了__分鐘.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線AB與正比例函數(shù)![]() 的圖象交于點
的圖象交于點![]() ,與y軸交于點
,與y軸交于點![]() .點P為直線OA上的動點,點P的橫坐標(biāo)為t,以點P為頂點,作長方形PDEF,滿足
.點P為直線OA上的動點,點P的橫坐標(biāo)為t,以點P為頂點,作長方形PDEF,滿足![]() 軸,且
軸,且![]() ,
,![]() .
.
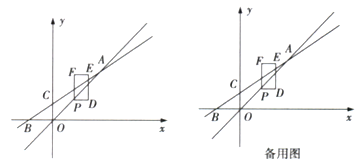
(1)求k的值及直線AB的函數(shù)表達(dá)式,并判定![]() 時,點E是否落在直線AB上;
時,點E是否落在直線AB上;
(2)在點P運動的過程中,當(dāng)點F落在直線AB上時,求t的值;
(3)在點P運動的過程中,若長方形PDEF與直線AB有公共點,求t的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,數(shù)軸上有三個點![]() 、
、![]() 、
、![]() ,表示的數(shù)分別是
,表示的數(shù)分別是![]() 、
、![]() 、3,請回答:
、3,請回答:
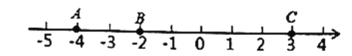
(1)若使![]() 、
、![]() 兩點的距離與
兩點的距離與![]() 、
、![]() 兩點的距離相等,則需將點
兩點的距離相等,則需將點![]() 向左移動_________個單位長度;
向左移動_________個單位長度;
(2)點![]() 、
、![]() 、
、![]() 開始在數(shù)軸上運動,若點
開始在數(shù)軸上運動,若點![]() 以每秒1個單位長度的速度向左運動,同時,點
以每秒1個單位長度的速度向左運動,同時,點![]() 和點
和點![]() 分別以每秒2個單位長度和5個單位長度的速度向右運動,運動
分別以每秒2個單位長度和5個單位長度的速度向右運動,運動![]() 秒鐘后:
秒鐘后:
①點![]() 、
、![]() 、
、![]() 表示的數(shù)分別是________、________、________(用含
表示的數(shù)分別是________、________、________(用含![]() 的式子表示);
的式子表示);
②若點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() .試問:
.試問:![]() 的值是否隨著時間
的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求出
的變化而改變?若變化,請說明理由;若不變,請求出![]() 值.
值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)數(shù) a , b , c 在數(shù)軸上的位置如圖 1 所示且| a || c |:

①填空:| a | , | b a | ,| 2b | .
②化簡:| c b | | b a | | a b | .
( 2) a , b , c 大小關(guān)系如圖 2, 下列各式① b a (c) 0 ; ② (a) b c 0 ;③![]() ④ bc a 0 ;⑤| a b | | c b | | a c | 2b ,其中正確的有 .
④ bc a 0 ;⑤| a b | | c b | | a c | 2b ,其中正確的有 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
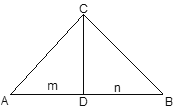
【題目】如圖,已知△ABC中,∠ACB=90°,過C點作CD⊥AB,垂足為D,且AD=m,BD= n,AC2:BC2=2:1,又關(guān)于x的方程![]() x2-2(n-1)x+m2-12=0,兩實數(shù)根的差的平方小于192,
x2-2(n-1)x+m2-12=0,兩實數(shù)根的差的平方小于192,
求:m,n為整數(shù)時,一次函數(shù)y=mx+n的解析式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com