【題目】如圖，直線y=﹣2x+4交x軸于點A，交y軸于點B，與反比例函數y=
的圖象有唯一的公共點C．
（1）求k的值及C點坐標；
（2）直線l與直線y=﹣2x+4關于x軸對稱，且與y軸交于點B'，與雙曲線y=
交于D、E兩點，求△CDE的面積．
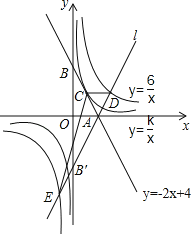
【答案】（1）k=2; C（1，2）；(2)8.
【解析】（1）令-2x+4=
，則2x2-4x+k=0，依據直線y=-2x+4與反比例函數y=的圖象有唯一的公共點C，即可得到k的值，進而得出點C的坐標；
（2）依據直線l與直線y=-2x+4關于x軸對稱，即可得到直線l為y=2x-4，再根據
=2x-4，即可得到E（-1，-6），D（3，2），可得CD=2，進而得出△CDE的面積=
×2×（6+2）=8．
（1）令-2x+4=，則2x2-4x+k=0，
∵直線y=-2x+4與反比例函數y=的圖象有唯一的公共點C，
∴△=16-8k=0，
解得k=2，
∴2x2-4x+2=0，
解得x=1，
∴y=2，
即C（1，2）；
（2）∵直線l與直線y=-2x+4關于x軸對稱，
∴A（2，0），B'（0，-4），
∴直線l為y=2x-4，
令=2x-4，則x2-2x-3=0，
解得x1=3，x2=-1，
∴E（-1，-6），D（3，2），
又∵C（1，2），
∴CD=3-1=2，
∴△CDE的面積=×2×（6+2）=8．
英才點津系列答案
紅果子三級測試卷系列答案科目：初中數學 來源： 題型：
【題目】依次剪6張正方形紙片拼成如圖示意的圖形，圖形中正方形①的面積為1，正方形②的面積為
．
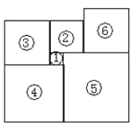
(1)請用含
的式子直接寫出正方形⑤的面積；
(2)若正方形⑥與正方形③的面積相等，求正方形④和正方形⑤的面積比．
查看答案和解析>>
科目：初中數學 來源： 題型：
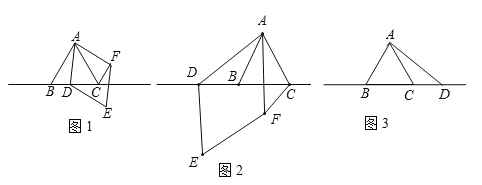
【題目】△ABC中，∠BAC=60°，AB=AC，點D為直線BC上一動點（點D不與B，C重合），以AD為邊在AD右側作菱形ADEF，使∠DAF=60°，連接CF．
（1）觀察猜想：如圖1，當點D在線段BC上時，①AB與CF的位置關系為： ；
②BC，CD，CF之間的數量關系為： ．
（2）數學思考：如圖2，當點D在線段CB的延長線上時，結論①，②是否仍然成立？若成立，請給予證明；若不成立，請你寫出正確結論再給予證明．
（3）拓展延伸：如圖3，當點D在線段BC的延長線上時，設AD與CF相交于點G，若已知AB=4，CD=
AB，求AG的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，
，AO是∠BAC的平分線，與AB的垂直平分線DO交于點O，∠ACB沿EF折疊后，點C 剛好與點O重合．下列結論錯誤的是（ ）
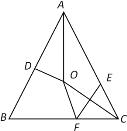
A.AO＝COB.∠ECO＝∠FCOC.EF⊥OCD.∠BFO＝2∠FOC
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，在△ABC中，BD平分∠ABC，CD平分∠ACB，BD，CD交于點D，EF過點D交AB于點E，交AC于點F．
（1）如圖1，若EF∥BC，則∠BDE＋∠CDF的度數為 （用含有∠A的代數式表示）；
（2）當直線EF繞點D旋轉到如圖2所示的位置時，（1）中的結論是否成立？請說明理由；
（3）當直線EF繞點D旋轉到如圖3所示的位置時，（1）中的結論是否成立？若成立，請說明理由；若不成立，請求出∠BDE，∠CDF與∠A之間的關系．
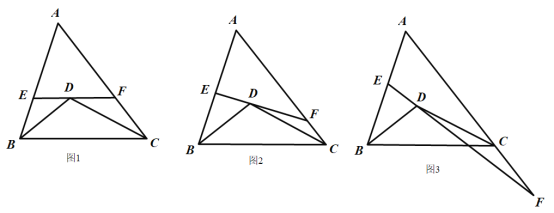
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線交x軸于A、B兩點，交y軸于C點，A點坐標為（﹣1，0），OC=2，OB=3，點D為拋物線的頂點．
（1）求拋物線的解析式；
（2）P為坐標平面內一點，以B、C、D、P為頂點的四邊形是平行四邊形，求P點坐標；
（3）若拋物線上有且僅有三個點M1、M2、M3使得△M1BC、△M2BC、△M3BC的面積均為定值S，求出定值S及M1、M2、M3這三個點的坐標．
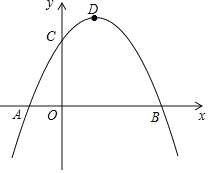
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法正確的是（ ）
A. 要了解某公司生產的100萬只燈泡的使用壽命，可以采用抽樣調查的方法
B. 4位同學的數學期末成績分別為100、95、105、110，則這四位同學數學期末成績的中位數為100
C. 甲乙兩人各自跳遠10次，若他們跳遠成績的平均數相同，甲乙跳遠成績的方差分別為0.51和0.62，則乙的表現較甲更穩定
D. 某次抽獎活動中，中獎的概率為
表示每抽獎50次就有一次中獎
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，四邊形AOBC是矩形，點O(0，0)，點A(5，0)，點B(0，3)．以點A為中心，順時針旋轉矩形AOBC，得到矩形ADEF，點O，B，C的對應點分別為D，E，F．
(Ⅰ)如圖①，當點D落在BC邊上時，求點D的坐標；
(Ⅱ)如圖②，當點D落在線段BE上時， AD與BC交于點H．
①求證△ADB≌△AOB；
②求點H的坐標．
(Ⅲ)記K為矩形AOBC對角線的交點，S為△KDE的面積，求S的取值范圍(直接寫出結果即可)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
