
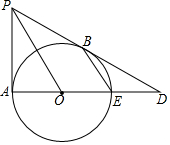
 如圖,PA,PB分別與⊙O相切于點(diǎn)A,B,延長(zhǎng)PB交直徑AE的延長(zhǎng)線于點(diǎn)D.
如圖,PA,PB分別與⊙O相切于點(diǎn)A,B,延長(zhǎng)PB交直徑AE的延長(zhǎng)線于點(diǎn)D.分析 (1)根據(jù)切線的性質(zhì)和直徑所對(duì)的圓周角等于90°,可以求得∠COA=∠BEA,從而可以證明結(jié)論成立;
(2)根據(jù)tan∠OPD=$\frac{1}{2}$,然后利用銳角三角函數(shù)和勾股定理、三角形相似可以求得tan∠D的值.
解答  (1)證明:連接AB,交PO于點(diǎn)C,如右圖所示,
(1)證明:連接AB,交PO于點(diǎn)C,如右圖所示,
∵PA,PB分別與⊙O相切于點(diǎn)A,B,延長(zhǎng)PB交直徑AE的延長(zhǎng)線于點(diǎn)D,
∴PC⊥AB,BE⊥AB,
∴∠ACO=∠ABE=90°,
∴∠CAO+∠AOC=90°,∠BAE+∠BEA=90°,
∴∠COA=∠BEA,
∴BE∥OP;
(2)連接BO,如右上圖所示,
設(shè)BC=a,
∵tan∠OPD=$\frac{1}{2}$,
∴PC=2a,
∴PB=$\sqrt{5}a$,
∵∠OPD=∠CBO,BC=a,tan∠OPD=$\frac{1}{2}$,
∴BO=$\frac{\sqrt{5}a}{2}$,
∴PO=$\frac{5a}{2}$,
∵AB⊥BE,AB=2a,AE=2BO=$\sqrt{5}a$,
∴BE=a,
∵BE∥PO,
設(shè)DB=x,
∴$\frac{DB}{DP}=\frac{BE}{PO}$,
即$\frac{x}{x+\sqrt{5}a}=\frac{a}{\frac{5a}{2}}$,
解得,x=$\frac{2\sqrt{5}a}{3}$,
∴tan∠D=$\frac{BO}{BD}$=$\frac{\frac{\sqrt{5}a}{2}}{\frac{2\sqrt{5}a}{3}}$=$\frac{3}{4}$.
點(diǎn)評(píng) 本題考查切線的性質(zhì)、解直角三角形,解答本題的關(guān)鍵是明確題意,找出所求問(wèn)題需要的條件,利用銳角三角函數(shù)、三角形相似的知識(shí)解答.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 測(cè)量體校籃球隊(duì)和排球隊(duì)中180名隊(duì)員的身高 | |
| B. | 隨機(jī)抽取本市一所學(xué)校的180名學(xué)生的身高 | |
| C. | 查閱有關(guān)外地180名學(xué)生身高的統(tǒng)計(jì)資料 | |
| D. | 在本地的市區(qū)和郊縣各任選一所完全中學(xué)、兩所初級(jí)中學(xué),在這六所學(xué)校的七、八、九年級(jí)的一個(gè)班中,用抽簽的方法分別選出10名學(xué)生,然后測(cè)量他們的身高. |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
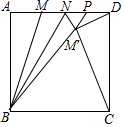 如圖,正方形ABCD的邊長(zhǎng)為6,AM=$\frac{1}{3}$AD,點(diǎn)N在線段MD上,連接BN,把△BMN沿BN翻折,得到△BM′N(xiāo),延長(zhǎng)BM′交線段DN于點(diǎn)P,連接CM′,DM′,當(dāng)△CDM′是等腰三角形時(shí),MN的長(zhǎng)為$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.
如圖,正方形ABCD的邊長(zhǎng)為6,AM=$\frac{1}{3}$AD,點(diǎn)N在線段MD上,連接BN,把△BMN沿BN翻折,得到△BM′N(xiāo),延長(zhǎng)BM′交線段DN于點(diǎn)P,連接CM′,DM′,當(dāng)△CDM′是等腰三角形時(shí),MN的長(zhǎng)為$\frac{131-24\sqrt{65}}{8}$或=$\frac{19\sqrt{31}+16}{54}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
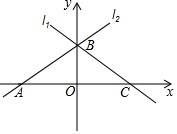 如圖,直線l1與直線l2關(guān)于y軸對(duì)稱(chēng),已知直線l1的函數(shù)表達(dá)式為y=-$\frac{4}{3}$x+b,點(diǎn)B 坐標(biāo)為(0,3),則點(diǎn)A坐標(biāo)為(-$\frac{9}{4}$,0).
如圖,直線l1與直線l2關(guān)于y軸對(duì)稱(chēng),已知直線l1的函數(shù)表達(dá)式為y=-$\frac{4}{3}$x+b,點(diǎn)B 坐標(biāo)為(0,3),則點(diǎn)A坐標(biāo)為(-$\frac{9}{4}$,0).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
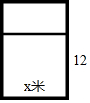 有12米長(zhǎng)的木條,要做成一個(gè)如圖的窗框,如果假設(shè)窗框橫檔的長(zhǎng)度為x米,那么窗框的面積是(木條的寬度忽略不計(jì))( )
有12米長(zhǎng)的木條,要做成一個(gè)如圖的窗框,如果假設(shè)窗框橫檔的長(zhǎng)度為x米,那么窗框的面積是(木條的寬度忽略不計(jì))( )| A. | x(6-$\frac{3}{2}$x)米2 | B. | x(12-x)米2 | C. | x(6-3x)米2 | D. | x(6-x)米2 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com