
 在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC為斜邊作等腰Rt△ACD,連接BD,則BD的長度為$\frac{\sqrt{62}}{2}$.
在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC為斜邊作等腰Rt△ACD,連接BD,則BD的長度為$\frac{\sqrt{62}}{2}$. 分析 以AB為腰作等腰Rt△ABE,連接EC,由△ADC為等腰Rt△知$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$、∠EAB=∠DAC=45°,結合∠EAB+∠BAC=∠BAC+∠DAC即∠EAC=∠DAB,證△EAC∽△BAD得$\frac{BD}{EC}$=$\frac{\sqrt{2}}{2}$,作EF⊥BC交BC延長線于F,知∠EBF=30°,從而求得EF=BEsin30°=$\frac{\sqrt{3}}{2}$,FB=BEcos30°=$\frac{3}{2}$,繼而得EC=$\sqrt{E{F}^{2}+F{C}^{2}}$=$\sqrt{31}$,根據BD=$\frac{\sqrt{2}}{2}$EC可得答案.
解答 解:以AB為腰作等腰Rt△ABE,連接EC,
∵△ADC為等腰Rt△,
∴$\frac{AD}{AC}$=$\frac{\sqrt{2}}{2}$,∠EAB=∠DAC=45°,
∴∠EAB+∠BAC=∠BAC+∠DAC,
∴∠EAC=∠DAB,
∴△EAC∽△BAD,
∴$\frac{BD}{EC}$=$\frac{\sqrt{2}}{2}$,
作EF⊥BC交BC延長線于F,
∵∠ABC=60°,∠EBA=90°,
∴∠EBF=30°,
∴EF=BEsin30°=$\frac{\sqrt{3}}{2}$,FB=BEcos30°=$\frac{3}{2}$,
∴EC=$\sqrt{E{F}^{2}+F{C}^{2}}$=$\sqrt{31}$,
∴BD=$\frac{\sqrt{2}}{2}$EC=$\frac{\sqrt{62}}{2}$,
故答案為:$\frac{\sqrt{62}}{2}$.
點評 本題主要考查了等腰直角三角形的判定與性質、相似三角形的判定與性質、勾股定理等重要知識點,有一定難度.正確作出輔助線是本題的難點.


 走進文言文系列答案
走進文言文系列答案科目:初中數學 來源:2017屆江蘇省無錫市九年級3月月考數學試卷(解析版) 題型:判斷題
某市今年的信息技術結業考試,采用學生抽簽的方式決定自己的考試內容.規定:每位考生先在三個筆試題(題簽分別用代碼B1、B2、B3表示)中抽取一個,再在三個上機題(題簽分別用代碼J1、J2、J3表示)中抽取一個進行考試.小亮在看不到題簽的情況下,分別從筆試題和上機題中隨機地抽取一個題簽.
(1)用樹狀圖或列表法表示出所有可能的結果;
(2)求小亮抽到的筆試題和上機題的題簽代碼的下標(例如“B1”的下標為“1”)為一個奇數一個偶數的概率.
查看答案和解析>>
科目:初中數學 來源:2017屆遼寧省丹東市九年級第一次模擬考試數學試卷(解析版) 題型:單選題
如圖,在△ABC中,AD和BE是高,∠ABE=45°,點F是AB的中點,AD與FE、BE分別交于點G、H,∠CBE=∠BAD.有下列結論:①FD=FE;②AH=2CD;③BC•AD=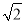 AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數為( )
AE2;④∠DFE=2∠DAC ;⑤若連接CH,則CH∥EF.其中正確的個數為( )
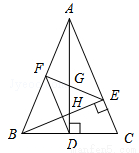
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
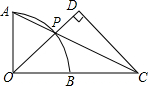 如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OB=BC=1,則PD的長為( )
如圖,點O為弧AB所在圓的圓心,OA⊥OB,點P在弧AB上,AP的延長線與OB的延長線交于點C,過點C作CD⊥OP于D.若OB=BC=1,則PD的長為( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com