
 如圖,一條船從燈塔C的南偏東42°的A處出發,向正北航行8海里到達B處,此時燈塔C在船的北偏西84°方向,則船距離燈塔C8海里.
如圖,一條船從燈塔C的南偏東42°的A處出發,向正北航行8海里到達B處,此時燈塔C在船的北偏西84°方向,則船距離燈塔C8海里. 分析 先利用平行線的性質得到∠A=∠ACD=42°,再利用三角形外角性質可求出∠ABC=42°,則∠ABC=∠A,于是可判斷△BAC為等腰三角形,所以BC=BA=8,
解答 解:如圖,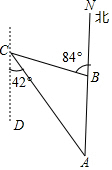 ∵AB∥CD,
∵AB∥CD,
∴∠A=∠ACD=42°,
∵∠NBC=∠A+∠ABC,
∴∠ABC=84°-42°=42°,
∴∠ABC=∠A,
∴BC=BA=8,
即船距離燈塔C8海里.
故答案為8.
點評 本題考查了等腰三角形的判定與性質:在等腰三角形有關問題中,會遇到一些添加輔助線的問題,其頂角平分線、底邊上的高、底邊上的中線是常見的輔助線,雖然“三線合一”,但添加輔助線時,有時作哪條線都可以,有時不同的做法引起解決問題的復雜程度不同,需要具體問題具體分析.也考查了方向角.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2017屆江蘇省無錫市九年級3月月考數學試卷(解析版) 題型:填空題
在平面直角坐標系中,點O為坐標原點,A、B、C三點的坐標為(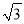 ,0)、(3
,0)、(3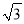 ,0)、(0,5),點D在第一象限,且∠ADB=60º,則線段CD的長的最小值為______.
,0)、(0,5),點D在第一象限,且∠ADB=60º,則線段CD的長的最小值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC為斜邊作等腰Rt△ACD,連接BD,則BD的長度為$\frac{\sqrt{62}}{2}$.
在△ABC中,AB=$\sqrt{3}$,BC=4,∠ABC=60°,以AC為斜邊作等腰Rt△ACD,連接BD,則BD的長度為$\frac{\sqrt{62}}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
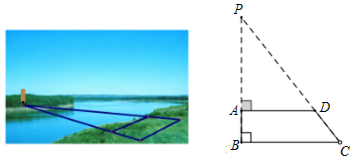
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com