
 如圖,AB為半圓O的直徑,AD、BC分別切⊙O于A,B兩點,CD切⊙O于點E,連接OD、OC,下列結論:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正確的有( )
如圖,AB為半圓O的直徑,AD、BC分別切⊙O于A,B兩點,CD切⊙O于點E,連接OD、OC,下列結論:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:OE,⑤OD2=DE•CD,正確的有( )| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
分析 連接OE,利用切線長定理得到DE=DA,CE=CB,由CD=DE+EC,等量代換可得出CD=AD+BC,選項②正確;由AD=ED,OD為公共邊,利用HL可得出直角三角形ADO與直角三角形EDO全等,可得出∠AOD=∠EOD,同理得到∠EOC=∠BOC,而這四個角之和為平角,可得出∠DOC為直角,選項①正確;由∠DOC與∠DEO都為直角,再由一對公共角相等,利用兩對對應角相等的兩三角形相似,可得出三角形DEO與三角形DOC相似,由相似得比例可得出OD2=DE•CD,選項⑤正確;由△AOD∽△BOC,可得選項③正確;由△ODE∽△OEC,可得選項④正確.
解答 解:連接OE,如圖所示:
∵AD與圓O相切,DC與圓O相切,BC與圓O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,選項②正確;
在Rt△ADO和Rt△EDO中,$\left\{\begin{array}{l}{OD=OD}\\{DA=DE}\end{array}\right.$,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,
即∠DOC=90°,選項①正確;
∴∠DOC=∠DEO=90°,
又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴$\frac{OD}{CD}=\frac{DE}{OD}$,即OD2=DC•DE,選項⑤正確;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴$\frac{{S}_{△AOD}}{{S}_{△BOC}}$=($\frac{AD}{OB}$)2=($\frac{AD}{AO}$)2=$\frac{A{D}^{2}}{A{O}^{2}}$,選項③正確;
同理△ODE∽△OEC,
∴OD:OC=DE:OE,選項④正確;
故選D.
點評 此題考查了切線的性質,切線長定理,相似三角形的判定與性質,全等三角形的判定與性質,利用了轉化的數學思想,熟練掌握切線長定理,證明三角形全等和三角形相似是解本題的關鍵.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
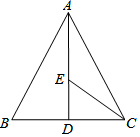 如圖所示,在等邊三角形ABC中,BC邊上的高AD=10,E是AD上一點,現有一動點P沿著折線A-E-C運動,在AE上的速度是4單位/秒,在CE上的速度是2單位/秒,則點P從A到C的運動過程中至少需5秒.
如圖所示,在等邊三角形ABC中,BC邊上的高AD=10,E是AD上一點,現有一動點P沿著折線A-E-C運動,在AE上的速度是4單位/秒,在CE上的速度是2單位/秒,則點P從A到C的運動過程中至少需5秒.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com