
分析 連接兩個(gè)已知點(diǎn)的線段有3條,作它們的垂直平分線,在這些垂直平分線及已知3個(gè)點(diǎn)外,任取一點(diǎn)O為圓心.設(shè)O到這3個(gè)已知的距離為d1,d2,d3,則它們兩兩不等且都大于0.接下來只要證明可以取得r0,r1,r2,r3為半徑的同心圓滿足所有的要求即可.
解答 證明:連接兩個(gè)已知點(diǎn)的線段有3條,作它們的垂直平分線,在這些垂直平分線及已知3個(gè)點(diǎn)外,任取一點(diǎn)O為圓心.
設(shè)O到這3個(gè)已知的距離為d1,d2,d3,則它們兩兩不等且都大于0.
不妨假設(shè)0<d1<d2<d3,則存在有理數(shù)r1,r2,r3,使得d1<r1<d2<r2<d3<r3,
將它們通分得r1=$\frac{{P}_{1}}{M}$,r2=$\frac{{P}_{2}}{M}$,r3=$\frac{{P}_{3}}{M}$,這里M是它們分母的公倍數(shù).
我們可以取M足夠大,使$\frac{1}{M}$<d1,
令r0=$\frac{1}{M}$,則以r0,r1,r2,r3為半徑的同心圓滿足所有的要求.
點(diǎn)評(píng) 本題考查圓綜合題、線段的垂直平分線的性質(zhì)、同心圓等知識(shí),解題的關(guān)鍵是理解題意,本題的突破點(diǎn)是取點(diǎn)O在這些垂直平分線及已知3個(gè)點(diǎn)外,這是關(guān)鍵,題目比較抽象,屬于屬于競賽題目.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{90}{x+2}$=$\frac{60}{x-2}$ | B. | $\frac{90}{x-2}$=$\frac{60}{x+2}$ | C. | $\frac{90}{x}$+2=$\frac{60}{x}$ | D. | $\frac{60}{x}$+2=$\frac{90}{x}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 23 | 6 | -3 | -4 | 3 | 18 | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
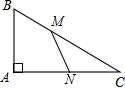 如圖,Rt△ABC中,∠A=90°,∠ABC=60°,AC=3,點(diǎn)M是邊BC上一點(diǎn),點(diǎn)N是邊AC上一點(diǎn)(不與點(diǎn)A、C重合),且MB=MN,則MB的取值范圍是$\frac{2\sqrt{3}}{3}$≤MB<$\sqrt{3}$.
如圖,Rt△ABC中,∠A=90°,∠ABC=60°,AC=3,點(diǎn)M是邊BC上一點(diǎn),點(diǎn)N是邊AC上一點(diǎn)(不與點(diǎn)A、C重合),且MB=MN,則MB的取值范圍是$\frac{2\sqrt{3}}{3}$≤MB<$\sqrt{3}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
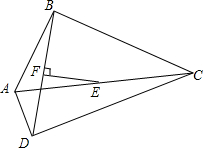 如圖,在四邊形ABCD中,E、F分別是AC、BD的中點(diǎn),EF⊥BD,點(diǎn)F為垂足,∠ADC=90°.求∠ABC的度數(shù).
如圖,在四邊形ABCD中,E、F分別是AC、BD的中點(diǎn),EF⊥BD,點(diǎn)F為垂足,∠ADC=90°.求∠ABC的度數(shù).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
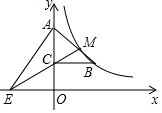 如圖,反比例函數(shù)y=$\frac{k}{x}$的圖象經(jīng)過Rt△ABC斜邊AB的中點(diǎn)M 及頂點(diǎn)B,點(diǎn)C在y軸正半軸上,連結(jié)MC并延長與x軸交于點(diǎn)E.
如圖,反比例函數(shù)y=$\frac{k}{x}$的圖象經(jīng)過Rt△ABC斜邊AB的中點(diǎn)M 及頂點(diǎn)B,點(diǎn)C在y軸正半軸上,連結(jié)MC并延長與x軸交于點(diǎn)E.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com