
 如圖,⊙O的半徑為4,△ABC是⊙O的內接三角形,連接OB、OC,若∠BAC與∠BOC互補,則弦BC的長為( )
如圖,⊙O的半徑為4,△ABC是⊙O的內接三角形,連接OB、OC,若∠BAC與∠BOC互補,則弦BC的長為( )| A. | 7$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 5$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
分析 作OH⊥BC于H,首先證明∠BOC=120,在Rt△BOH中,BH=OB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,即可推出BC=2BH=4$\sqrt{3}$,
解答 解:作OH⊥BC于H.
∵∠BOC=2∠BAC,∠BOC+∠BAC=180°,
∴∠BOC=120°,
∵OH⊥BC,OB=OC,
∴BH=HC,∠BOH=∠HOC=60°,
在Rt△BOH中,BH=OB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BC=2BH=4$\sqrt{3}$,
故選D.
點評 本題考查三角形的外接圓與外心、銳角三角函數、垂徑定理等知識,解題的關鍵是學會添加常用輔助線,還在直角三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
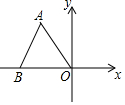 等邊△ABO在平面直角坐標系內的位置如圖所示,已知△ABO的邊長為6,則點A的坐標為( )
等邊△ABO在平面直角坐標系內的位置如圖所示,已知△ABO的邊長為6,則點A的坐標為( )| A. | (-3,3) | B. | (3,-3$\sqrt{3}$) | C. | (-3,3$\sqrt{3}$) | D. | (-3,-3$\sqrt{3}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 服裝統一 | 進退場有序 | 動作規范 | 動作整齊 | |
| 一班 | 80 | 84 | 88 | 84 |
| 二班 | 97 | 78 | 80 | 85 |
| 三班 | 90 | 78 | 84 | 84 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com