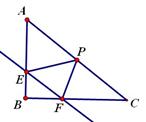
已知Rt△ABC,∠B=90°，直線EF分別于兩直角邊AB、AC交于E、F兩點，且EF//AC。P是斜邊AC的中點，連接PE、PF，且已知AB=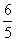
,BC=
。
（1） 如圖1，當E、F均為兩直角邊中點時，求證：四邊形EPFB是矩形，并求出此時EF的長。
（2） 如圖2，設EF的長度為x（x>0）,當sin∠EPF=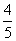
（∠EPF為銳角）時，用含x的代數式表示EP的長度。
（3） 記△PEF 的面積為S，則當EP為多少時，S的值最大，并求出該最大值。
時刻準備著暑假作業原子能出版社系列答案科目：初中數學 來源： 題型：
為了節約資源，科學指導居民改善居住條件，小王向房管部門提出了一個購買商品房的政策性方案.
| 人均住房面積（平方米） | 單 |
| 不超過30（平方米） | 0.3 |
| 超過30平方米不超過 | 0.5 |
| 超過 | 0.7 |
根據這個購房方案：
⑴若某三口之家欲購買120平方米的商品房，求其應繳納的房款；
⑵設該家庭購買商品房的人均面積為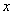
平方米，繳納房款y萬元，請求出
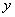關于x的
函數關系式；
⑶若該家庭購買商品房的人均面積為50平方米，繳納房款為y萬元，且 57<y≤60 時，
求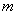
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
親愛的同學，你能比較20092010和20102009的大小嗎？為了解決這個問題，我們先把它抽象成數學問題，寫出它的一般形式，即比較nn+1和（n+1）n的大小（n是自然數）然后，我們分析n=1,n=2,n=3…這些簡單情形入手，從中發現規律，經過歸納、猜想，得出結論。
(1)通過計算，比較下列各組中兩個數的大小（在空格中選填 ﹤﹥﹦ 號）
12 ﹤ 21 23 ﹤ 32 34 ﹤ 43 45 ﹤ 54 56 ﹤ 65…
(2)從第（1）小題的結果，經過歸納，可以猜想出nn+1和（n+1）n的大小關系是
（3）根據上面歸納猜想得到的一般結論，試比較下列兩個數的大小：20102011 20112010
查看答案和解析>>
科目：初中數學 來源： 題型：
某校對初三（2）班40名學生體育考試中“立定跳遠”項目的得分情況進行了統計，結果如下表，
| 得 分 | 10分 | 9分 | 8分 | 7分 | 6分以下 |
| 人數（人） | 20 | 12 | 5 | 2 | 1 |
根據表中數據，若隨機抽取該班的一名學生，則該學生“立定跳遠”得分恰好是10分的概率是 。
查看答案和解析>>
科目：初中數學 來源： 題型：
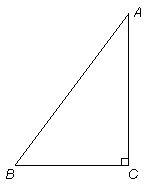
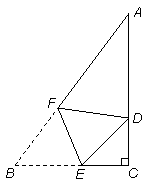
如圖，三角形紙片ABC中，∠C＝90°，AC＝4，BC＝3．將紙片折疊，使點B落在AC邊上的點D處，折痕與BC、AB分別交于點E、F．
（1）設BE＝x，DC＝y，求y關于x的函數關系式，并確定自變量x的取值范圍；
（2）當△ADF是直角三角形時，求BE的長；
（3）當△ADF是等腰三角形，且∠A是頂角時，求BE的長。
 |  | ||
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
……………矩形 ，EF 
價（萬元/平方米）
,②2a-2b ,③ 
中任意選取兩個代數式構造分式，然后進行化簡，并求當a、b為不等式組
整數解，且a>b時的值。
A．
B．
C．
D．