
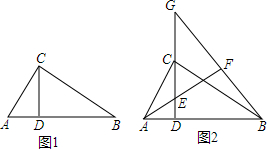
 如圖1,△ABC中,∠ACB=90°,CD⊥AB,垂足為D;
如圖1,△ABC中,∠ACB=90°,CD⊥AB,垂足為D;分析 (1)根據垂直的定義得到∠ADC=∠CDB=90°,根據余角的性質得到∠ACD=∠B,由于∠ADC=∠CDB,即可得到結論;
(2)根據∠ACB=90°,CD⊥AB,得到∠CAD=∠BCD,推出Rt△ACD∽Rt△CBD,于是得到CD2=AD•BD,根據AF⊥BG,GD⊥AB,證得∠EDA=∠EFG=∠GDP=90°,推出△BGD∽△ADE,于是得到AD•BD=DG•DE即可得到結論.
解答 證明:(1)∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∴∠BCD+∠B=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠ACD=∠B,
又∵∠ADC=∠CDB,
∴△ACD∽△CBD;
(2)∵AF⊥BG,
∴∠AFB=90°,
∴∠FAB+∠GBA=90°,
∵∠GDB=90°,
∴∠G+∠GBA=90°,
∴∠G=∠FAB,
又∵∠ADE=∠GDB=90°,
∴△ADE∽△GDB,
∴$\frac{AD}{GD}=\frac{DE}{BD}$,
∴AD•BD=DE•DG,
∵△ACD∽△CBD,
∴$\frac{AD}{CD}=\frac{CD}{BD}$,
∴CD2=AD•BD,
∴CD2=DE•DG.
點評 此題主要考查的是相似三角形的判定和性質,垂直的定義,熟練掌握相似三角形的判定和性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
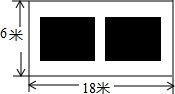 某小區在綠化工程中有一塊長為18m、寬為6m的矩形空地,計劃在其中修建兩塊相同的矩形綠地,使它們的面積之和為60m2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),求人行通道的寬度.
某小區在綠化工程中有一塊長為18m、寬為6m的矩形空地,計劃在其中修建兩塊相同的矩形綠地,使它們的面積之和為60m2,兩塊綠地之間及周邊留有寬度相等的人行通道(如圖所示),求人行通道的寬度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1條 | B. | 2條 | C. | 3條 | D. | 4條 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
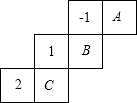 如圖是一個正方體的包裝盒的展開圖,若在其中的三個正方形A、B、C內分別填上適當的數,使得將這個展開圖沿虛線折成正方體后,相對面上的兩個數互為相反數,則填在A、B、C內的三個數依次是( )
如圖是一個正方體的包裝盒的展開圖,若在其中的三個正方形A、B、C內分別填上適當的數,使得將這個展開圖沿虛線折成正方體后,相對面上的兩個數互為相反數,則填在A、B、C內的三個數依次是( )| A. | -1,-2,1 | B. | -1,1,-2 | C. | -2,-1,1 | D. | 1,-1,-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
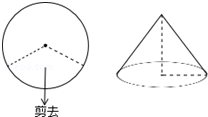 如圖,圣誕節快到了,小雪準備在一塊半徑為9cm的 紅布上剪掉三分之一圓周,然后用剩下的部分做成一個圣誕帽,則這個圣誕帽的高為3$\sqrt{5}$cm.
如圖,圣誕節快到了,小雪準備在一塊半徑為9cm的 紅布上剪掉三分之一圓周,然后用剩下的部分做成一個圣誕帽,則這個圣誕帽的高為3$\sqrt{5}$cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com