
【題目】如圖,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求證:CD⊥AB

【答案】見解析;
【解析】
靈活運用垂直的定義,注意由垂直可得90°角,由90°角可得垂直,結(jié)合平行線的判定和性質(zhì),只要證得∠ADC=90°,即可得CD⊥AB.
證明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定義),
∴ DG∥AC(同位角相等,兩直線平行).
∴ ∠2=∠ACD(兩直線平行,內(nèi)錯角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代換),
∴ EF∥CD(同位角相等,兩直線平行).
∴ ∠AEF=∠ADC(兩直線平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定義),
∴ ∠ADC=90°(等量代換).
∴ CD⊥AB(垂直的定義).


科目:初中數(shù)學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在直線
在直線![]() 上(
上(![]() ,
,![]() 除外),
除外),![]() 的垂線
的垂線![]() 與
與![]() 的垂線
的垂線![]() 交于點
交于點![]() ,研究
,研究![]() 和
和![]() 的數(shù)量關系.
的數(shù)量關系.
(1)在探究![]() ,
,![]() 的關系時,運用“從特殊到一般”的數(shù)學思想,發(fā)現(xiàn)當點
的關系時,運用“從特殊到一般”的數(shù)學思想,發(fā)現(xiàn)當點![]() 是
是![]() 的中點時,只需要取
的中點時,只需要取![]() 邊的中點
邊的中點![]() (如圖),通過推理證明就可以得到
(如圖),通過推理證明就可以得到![]() 的數(shù)量關系,請你按照這種思路直接寫出
的數(shù)量關系,請你按照這種思路直接寫出![]() 和
和![]() 的數(shù)量關系:_____________________
的數(shù)量關系:_____________________

(2)當點![]() 是線段
是線段![]() 上(
上(![]() ,
,![]() 除外)任意一點(其它條件不變),上面得到的結(jié)論是否仍然成立呢?證明你的結(jié)論;
除外)任意一點(其它條件不變),上面得到的結(jié)論是否仍然成立呢?證明你的結(jié)論;

(3)點![]() 在線段
在線段![]() 的延長線上,上面得到的結(jié)論是否仍然成立呢?在下圖中畫出圖形,并證明你的結(jié)論.
的延長線上,上面得到的結(jié)論是否仍然成立呢?在下圖中畫出圖形,并證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,⊙I為△ABC的內(nèi)切圓,點O為△ABC的外心,BC=6,AC=8.
(1)求⊙I的半徑;
(2)求線段OI的長.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 為正三角形,點
為正三角形,點![]() 、
、![]() 分別在菱形的邊
分別在菱形的邊![]() 、
、![]() 上滑動,且
上滑動,且![]() 、
、![]() 不與
不與![]() 、
、![]() 、
、![]() 重合.
重合.

(1)證明不論![]() 、
、![]() 在
在![]() 、
、![]() 上如何滑動,總有
上如何滑動,總有![]() ;
;
(2)當點![]() 、
、![]() 在
在![]() 、
、![]() 上滑動時,分別探討四邊形
上滑動時,分別探討四邊形![]() 和
和![]() 的面積是否發(fā)生變化?如果不變,求出這個定值;如果變化,求出最大(或最小)值.
的面積是否發(fā)生變化?如果不變,求出這個定值;如果變化,求出最大(或最小)值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,矩形ABCD 和正方形ECGF,其中E、H分別為AD、BC中點,連結(jié)AF、HG、AH.

(1)求證:![]() ;
;
(2)求證:![]() ;
;
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】佳佳某天上午9時騎自行車離開家,17時回家,他有意描繪了離家的距離與時同的變化情況,如圖所示.
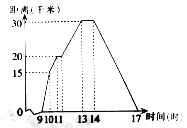
(1)圖象表示了哪兩個變量的關系?
(2)10時和11時,他分別離家多遠?
(3)他最初到達離家最遠的地方是什么時間?離家多遠?
(4)11時到13時他行駛了多少千米?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在 Rt△ABC 中,∠BAC=90°,AC=AB,點 F 是射線 CA 上一點,連接 BF,過 C 作 CE⊥BF,垂足為點 E,直線 CE,AB 相交于點 D.
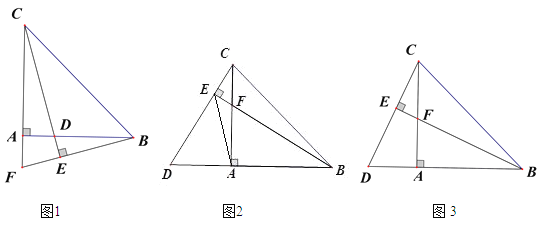
(1)如圖 1,當點 F 在線段 CA 延長線上時,求證:AB+AD=CF;
(2)如圖 2,當點 F 在線段 CA 上時,連接 EA,求證:EA 平分∠DEB;
(3)如圖 3,當點 F 恰好為線段 CA 的中點時,EF=1,試求△BDE 的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(1)①如圖1,已知![]() ,
,![]() ,可得
,可得![]() __________.
__________.

②如圖2,在①的條件下,如果![]() 平分
平分![]() ,則
,則![]() __________.
__________.

③如圖3,在①、②的條件下,如果![]() ,則
,則![]() __________.
__________.

(2)嘗試解決下面問題:已知如圖4,![]() ,
,![]() ,
,![]() 是
是![]() 的平分線,
的平分線,![]() ,求
,求![]() 的度數(shù).
的度數(shù).

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com