
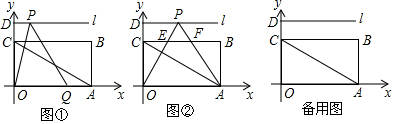
分析 (1)由四邊形OABC是矩形,根據矩形的性質,即可求得點B的坐標;由正切函數,即可求得∠CAO的度數;
(2)求出△POA的面積,證明△PEF∽△POA,由對應高的比等于相似比得出相似比,求出面積比,即可得出四邊形的面積;
(3)分別從MN=AN,AM=AN與AM=MN去分析求解即可求得答案.
解答 解:(1)∵四邊形OABC是矩形,
∴AB=OC,OA=BC,OA∥BC,
∵A(6,0)、C(0,2$\sqrt{3}$),
∴點B的坐標為:(6,2$\sqrt{3}$);
故答案為:(6,2$\sqrt{3}$);30°;
②∵tan∠CAO=$\frac{OC}{OA}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$,
∴∠CAO=30°
故答案為:(6,2$\sqrt{3}$);30;
(2)△POA的面積=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,
∵OA∥BC,
∴△PEF∽△POA,相似比為$\frac{DC}{DO}$=$\frac{3\sqrt{3}-2\sqrt{3}}{3\sqrt{3}}$=$\frac{1}{3}$,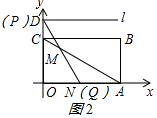
∴$\frac{{S}_{△PWF}}{{S}_{△POA}}$=$\frac{1}{9}$,
∴四邊形OEFQ的面積=$\frac{8}{9}$S△POA=$\frac{8}{9}$×9$\sqrt{3}$=8$\sqrt{3}$;
(3)設DP的長為m,分情況討論:
①如圖2,MN=AN=3時,
則∠AMN=∠MAN=30°,
∴∠MNO=60°,
∵∠PQO=60°,
即∠MQO=60°
∴點N與Q重合,
∴點P與D重合,
∴此時DP=0;
②如圖3,AM=AN時,作MJ⊥x軸于J、PI⊥x軸于I;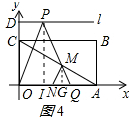
MJ=MQ•sin60°=AQ•sin60°=(OA-IQ-OI)•sin60°=$\frac{\sqrt{3}}{2}$(3-m)=$\frac{1}{2}$AM=$\frac{1}{2}$AN=$\frac{3}{2}$,
可得$\frac{\sqrt{3}}{2}$(3-m)
解得:m=3-$\sqrt{3}$;
③AM=NM時,此時M的橫坐標是4.5,
如圖4,過點P作PI⊥OA于I,過點M作MG⊥OA于G,
∴MG=$\frac{\sqrt{3}}{2}$,
∴QI=$\frac{PI}{tan60°}$=$\frac{3\sqrt{3}}{\sqrt{3}}$=3,GQ=$\frac{MG}{tan60°}$=$\frac{1}{2}$,
∴IG=3-0.5=2.5,AG=$\frac{1}{2}$AN=1.5,
∴OI=2,
∴m=2.
綜上所述:存在點P,使△MNA為等腰三角形,線段DP的長為0或3-$\sqrt{3}$或2.
點評 此題是四邊形綜合題目,考查了矩形的性質,相似三角形的判定與性質、等腰三角形的性質以及直角三角形的性質等知識.此題綜合性較強,難度較大,注意數形結合思想與分類討論思想的應用.


科目:初中數學 來源: 題型:選擇題
| A. | 若a=0,則ab=0 | |
| B. | 內錯角相等,兩直線平行 | |
| C. | 若兩個角相等,那么這兩個角都為30° | |
| D. | 若|a|=|b|,則a=b |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,小明在操場上畫了一個半徑分別為1,2,3的同心圓的圖案,現在往這個圖案中隨機扔一顆石子,這顆石子恰好落在區域C中的概率是( )
如圖,小明在操場上畫了一個半徑分別為1,2,3的同心圓的圖案,現在往這個圖案中隨機扔一顆石子,這顆石子恰好落在區域C中的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
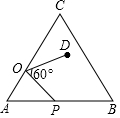 如圖,在等邊△ABC中,AC=9,點O在AC上,且AO=3,點P是AB上一動點,連結OP,將線段OP繞點O逆時針旋轉60°得到線段OD,要使點D恰好落在BC上,則AP的長是( )
如圖,在等邊△ABC中,AC=9,點O在AC上,且AO=3,點P是AB上一動點,連結OP,將線段OP繞點O逆時針旋轉60°得到線段OD,要使點D恰好落在BC上,則AP的長是( )| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com