
 如圖,過x軸上一點A作平行于y軸的直線分別與拋物線y=$\frac{1}{4}$x2及y=x2交于B、C兩點,若正方形BCDE的一邊DE與y軸重合,則此正方形BCDE的面積為$\frac{16}{9}$.
如圖,過x軸上一點A作平行于y軸的直線分別與拋物線y=$\frac{1}{4}$x2及y=x2交于B、C兩點,若正方形BCDE的一邊DE與y軸重合,則此正方形BCDE的面積為$\frac{16}{9}$. 分析 根據題意可以求得點B和點C的坐標,從而可以得到點B到y軸的距離等于線段BC的長,從而可以求得正方形的邊長,進而求得正方形的面積.
解答 解:設點A的坐標為(a,0),
由題意可得,點B的坐標為(a,$\frac{1}{4}$a2),點C的坐標為(a,a2),
∴a=a2-$\frac{1}{4}{a}^{2}$,
解得,a1=0(舍去),a2=$\frac{4}{3}$,
∴正方形BCDE的面積是:$\frac{4}{3}×\frac{4}{3}=\frac{16}{9}$,
故答案為:$\frac{16}{9}$.
點評 本題考查二次函數圖象上點的坐標特征、正方形的性質,解題的關鍵是明確題意,求出正方形的邊長.


 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:解答題
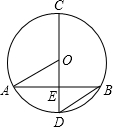 已知:如圖,在⊙O中,直徑CD交弦AB于點E,且CD平分弦AB,連接OA,BD.
已知:如圖,在⊙O中,直徑CD交弦AB于點E,且CD平分弦AB,連接OA,BD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
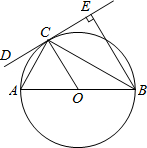 如圖,AB是⊙O的直徑,CD是⊙O的切線,切點為C,BE⊥CD,垂足為E,連接AC、BC.
如圖,AB是⊙O的直徑,CD是⊙O的切線,切點為C,BE⊥CD,垂足為E,連接AC、BC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
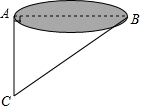 如圖,某學校數學課外活動小組的同學們,為了測量一個小湖泊兩岸的兩棵樹A和B之間的距離,在垂直AB的方向AC上確定點C,如果測得AC=75米,∠ACB=55°,那么A和B之間的距離是( )米.
如圖,某學校數學課外活動小組的同學們,為了測量一個小湖泊兩岸的兩棵樹A和B之間的距離,在垂直AB的方向AC上確定點C,如果測得AC=75米,∠ACB=55°,那么A和B之間的距離是( )米.| A. | 75•sin55° | B. | 75•cos55° | C. | 75•tan55° | D. | $\frac{75}{tan55°}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com