
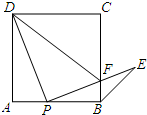
 如圖,點P是正方形ABCD邊AB上一點(點P不與點A,B重合),連接PD,將線段PD繞點P順時針方向旋轉90°得到線段PE,PE交邊BC于點F,連接BE,DF.
如圖,點P是正方形ABCD邊AB上一點(點P不與點A,B重合),連接PD,將線段PD繞點P順時針方向旋轉90°得到線段PE,PE交邊BC于點F,連接BE,DF.分析 (1)過E作EQ⊥AB交AB的延長線于Q,由旋轉得到PD=PE,∠1=90°,由四邊形ABCD是正方形,得到∠A=∠ABC=90°,AD=AB根據余角的性質得到∠2=∠4,根據全等三角形的性質得到EQ=AP,AD=AB=PQ,得到AP=EQ=BQ,于是得到結論;
(2)根據相似三角形的性質得到$\frac{PD}{BP}=\frac{PF}{BF}$,推出△APD∽△BFP,根據相似三角形的性質得到$\frac{AP}{BF}=\frac{PD}{FP}$,等量代換得到$\frac{PD}{BP}=\frac{PD}{AP}$,于是得到結論.
解答  解:(1)過E作EQ⊥AB交AB的延長線于Q,由旋轉得到PD=PE,∠1=90°,
解:(1)過E作EQ⊥AB交AB的延長線于Q,由旋轉得到PD=PE,∠1=90°,
∵四邊形ABCD是正方形,
∴∠A=∠ABC=90°,AD=AB,
∴∠EQP=∠A=90°,
∵∠2+∠3=90°,∠3+∠4=90°,
∴∠2=∠4,
在△PAD與△EQP中,$\left\{\begin{array}{l}{∠2=∠4}\\{∠A=∠Q}\\{PD=PE}\end{array}\right.$,
∴△PAD≌△EQP,
∴EQ=AP,AD=AB=PQ,
∴AP=EQ=BQ,
∴∠5=45°,
∴∠PBE=180°-∠5=135°;
(2)∵△PFD∽△BFP,
∴$\frac{PD}{BP}=\frac{PF}{BF}$,
∵∠A=∠PBC,∠2=∠4,
∴△APD∽△BFP,
∴$\frac{AP}{BF}=\frac{PD}{FP}$,即$\frac{FP}{BF}=\frac{PD}{AP}$,
∴$\frac{PD}{BP}=\frac{PD}{AP}$,
∴AP=BP,
∴$\frac{AP}{AB}=\frac{1}{2}$.
點評 本題主要考查的是全等三角形的性質和判定、相似三角形的判定、正方形的性質,證得△DAP≌△PGE是解題的關鍵.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案 品學雙優卷系列答案
品學雙優卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 8 | B. | 3 | C. | 2 | D. | 0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 11×103 | B. | 0.11×105 | C. | 1.1×103 | D. | 1.1×104 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
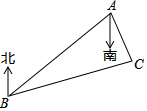 如圖,C島在A島的南偏東15°方向,C島在B島的北偏東70°方向,從C島看A、B兩島的視角∠ACB的度數是( )
如圖,C島在A島的南偏東15°方向,C島在B島的北偏東70°方向,從C島看A、B兩島的視角∠ACB的度數是( )| A. | 95° | B. | 85° | C. | 60° | D. | 40° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com