
 勾股定理是世界上最偉大的定理之一,是用代數思想解決幾何問題的重要工具,也是數形結合的紐帶,周老師在上八年級《從勾股定理到圖形面積關系的拓展》一節拓展課時,教學環節清晰,內容安排有序,問題設計合理(如下),作為課堂主人的你,請積極思考解決下列問題:
勾股定理是世界上最偉大的定理之一,是用代數思想解決幾何問題的重要工具,也是數形結合的紐帶,周老師在上八年級《從勾股定理到圖形面積關系的拓展》一節拓展課時,教學環節清晰,內容安排有序,問題設計合理(如下),作為課堂主人的你,請積極思考解決下列問題:分析 問題探究:(1)結論:S1+S2=S3,利用圓面積公式以及勾股定理即可證明.
(2)等邊三角形.利用等邊三角形的面積以及勾股定理即可證明.
拓展應用:(1)利用問題探究中的結論即可解決問題.
(2)根據S1+S2=$\frac{1}{2}$π(AB)2+$\frac{1}{2}$π($\frac{1}{2}$AC)2-$\frac{1}{2}$π($\frac{1}{2}$BC)2+S△ABC=$\frac{1}{8}$π(BC2+AC2-AB2)+S△ABC=S△ABC計算即可.
解答 解:問題探究:(1)結論:S1+S2=S3.理由如下:
∵S3=$\frac{π}{8}$c2,S2=$\frac{π}{8}$b2,S1=$\frac{π}{8}$a2,a2+b2=c2,
∴S1+S2=S3.
故答案為S1+S2=S3.
(2)等邊三角形或等腰直角三角形.
如圖3中,以直角三角形的三條邊a,b,c為邊,向外作等邊三角形,如圖所示,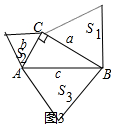
∵S1=$\frac{\sqrt{3}}{4}$a2,S2=$\frac{\sqrt{3}}{4}$b2,S3=$\frac{\sqrt{3}}{4}$c2,a2+b2=c2,
∴S2+S3=S1.
等腰三角形時證明方法類似.
故答案為等邊三角形或等腰直角三角形.
拓展應用:(1)如圖2中,∵S1+S2=S3,S3=$\frac{π}{8}$c2=$\frac{π}{8}$×16=2π.
故答案為2π.
2)解:如圖5中,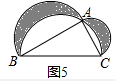
△ABC中,∵AB2+AC2=BC2
∴S1+S2=$\frac{1}{2}$π(AB)2+$\frac{1}{2}$π($\frac{1}{2}$AC)2-$\frac{1}{2}$π($\frac{1}{2}$BC)2+S△ABC=$\frac{1}{8}$π(BC2+AC2-AB2)+S△ABC=S△ABC=$\frac{1}{2}$×3×4=6.
故答案為6.
點評 此題主要涉及的知識點:三角形、正方形、圓的面積計算以及勾股定理的應用,解題關鍵是熟練掌握勾股定理的公式,學會用割補法求陰影部分面積,屬于中考常考題型..


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源:2017屆湖南津市中考數學模擬試卷(2)(解析版) 題型:單選題
在平面直角坐標系中直線y=x+2與反比例函數 的圖像有唯一公共點,若直線y=x+m與反比例函數
的圖像有唯一公共點,若直線y=x+m與反比例函數 的圖像有2個公共點,則m的取值范圍是( )
的圖像有2個公共點,則m的取值范圍是( )
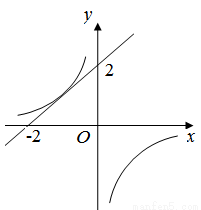
A. m>2 B. -2<m<2
C. m<-2 D. m>2或m<-2
查看答案和解析>>
科目:初中數學 來源:2016-2017學年四川省南充市度上學期八年級第二次月考數學試卷(解析版) 題型:填空題
如圖,在ABC中,AP=DP,DE=DF,DE⊥AB于E,DF⊥AC于F,則下列結論:①.AD平分∠BAC;②.△BED≌△FPD;③.DP∥AB;④.DF是PC的垂直平分線.其中正確的是= _________ .(寫序號)
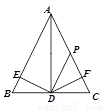
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,設線段AC=1.過點C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:連結AD,以點D為圓心,DC的長為半徑畫弧,交AD于點E;再以點A為圓心,AE的長為半徑畫弧,交AC于點B,則AB的長為( )
如圖,設線段AC=1.過點C作CD⊥AC,并且使CD=$\frac{1}{2}$AC:連結AD,以點D為圓心,DC的長為半徑畫弧,交AD于點E;再以點A為圓心,AE的長為半徑畫弧,交AC于點B,則AB的長為( )| A. | $\frac{2\sqrt{5}-1}{5}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{4}$ | D. | $\frac{\sqrt{5}+1}{4}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
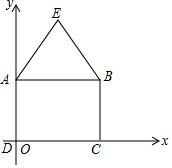 如圖所示,在長方形ABCD中,已知AB=6,AD=4,在長方形ABCD外畫△ABE,使AE=BE=5,請建立適當的平面直角坐標系,并求出各頂點的坐標.
如圖所示,在長方形ABCD中,已知AB=6,AD=4,在長方形ABCD外畫△ABE,使AE=BE=5,請建立適當的平面直角坐標系,并求出各頂點的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,△ABC內接于⊙O,D是弧BC的中點,OD交BC于點H,且OH=DH,連接AD,過點B作BE⊥AD于點E,連接EH,BF⊥AC于M,若AC=5,EH=$\frac{3}{2}$,則AF=$\frac{7\sqrt{3}}{3}$.
如圖,△ABC內接于⊙O,D是弧BC的中點,OD交BC于點H,且OH=DH,連接AD,過點B作BE⊥AD于點E,連接EH,BF⊥AC于M,若AC=5,EH=$\frac{3}{2}$,則AF=$\frac{7\sqrt{3}}{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com