
分析 (1)根據例題可得:對每個式子的分子和分母中同時乘以與分母中的式子相乘符合平方差公式的根式,去掉分母,然后合并同類二次根式即可求解;
(2)首先化簡a,然后把所求的式子化成4(a-1)2代入求解即可.
解答 解:(1)原式=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}$-$\sqrt{3}$)+…+($\sqrt{100}$-$\sqrt{99}$)=$\sqrt{100}$-1=10-1=9;
(2)a=$\sqrt{2}$+1,
則原式=4(a2-2a+1)-3=4(a-1)2,
當a=$\sqrt{2}$+1時,原式=4×($\sqrt{2}$)2=8.
點評 本題考查了二次根式的化簡求值,正確讀懂例題,對根式進行化簡是關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
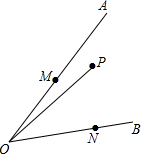 如圖:點P是∠AOB內一定點,點M、N分別在邊OA、OB上運運,若∠AOB=45°,OP=2$\sqrt{2}$,則△PMN的周長的最小值為4.
如圖:點P是∠AOB內一定點,點M、N分別在邊OA、OB上運運,若∠AOB=45°,OP=2$\sqrt{2}$,則△PMN的周長的最小值為4.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x-(y-z)=x-y-z | B. | -(x-y+z)=-x-y+z | ||
| C. | x+2y+2z=x-2(y+z) | D. | -a+c+d-b=-(a+b)+(c+d) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com