
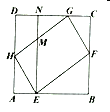
【題目】如圖,平行四邊形![]() 的四個頂點分別在正方形
的四個頂點分別在正方形![]() 的四條邊上.
的四條邊上.![]() ,分別交
,分別交![]() ,
,![]() ,
,![]() 于點
于點![]() ,
,![]() ,
,![]() ,且
,且![]() .要求得平行四邊形
.要求得平行四邊形![]() 的面積,只需知道一條線段的長度.這條線段可以是( )
的面積,只需知道一條線段的長度.這條線段可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
根據圖形證明△AOE≌△COG,作KM⊥AD,證明四邊形DKMN為正方形,再證明Rt△AEH≌Rt△CGF,Rt△DHG≌Rt△BFE,設正方形![]() 邊長為a,CG=MN=x,根據正方形的性質列出平行四邊形
邊長為a,CG=MN=x,根據正方形的性質列出平行四邊形![]() 的面積的代數式,再化簡整理,即可判斷.
的面積的代數式,再化簡整理,即可判斷.
連接AC,EG,交于O點,
∵四邊形![]() 是平行四邊形,四邊形
是平行四邊形,四邊形![]() 是正方形,
是正方形,
∴GO=EO,AO=CO,
又∠AOE=∠COG
∴△AOE≌△COG,
∴GC=AE,
∵NE∥AD,
∴四邊形AEND為矩形,
∴AE=DN,
∴DN=GC=MN
作KM⊥AD,
∴四邊形DKMN為正方形,
在Rt△AEH和Rt△CGF中,
![]()
∴Rt△AEH≌Rt△CGF,
∴AH=CF,
∵AD-AH=BC-CF
∴DH=BF,
同理Rt△DHG≌Rt△BFE,
設CG=MN=x,
設正方形![]() 邊長為a
邊長為a
則S△HDG=![]() DH×x+
DH×x+![]() DG×x=S△FBE
DG×x=S△FBE
S△HAE=![]() AH×x =S△GCF
AH×x =S△GCF
S平行四邊形EFGH=a2-2S△HDG-2S△HAE= a2-(DH+DG+AH)×x,
∵DG=a-x
∴S平行四邊形EFGH= a2-(a+a-x)×x= a2-2ax+x2= (a-x)2
故只需要知道a-x就可以求出面積
BE=a-x,故選C.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() 與
與![]() 軸左側拋物線交于點
軸左側拋物線交于點![]() ,直線
,直線![]() 與
與![]() 軸右側拋物線交于點
軸右側拋物線交于點![]() .
.
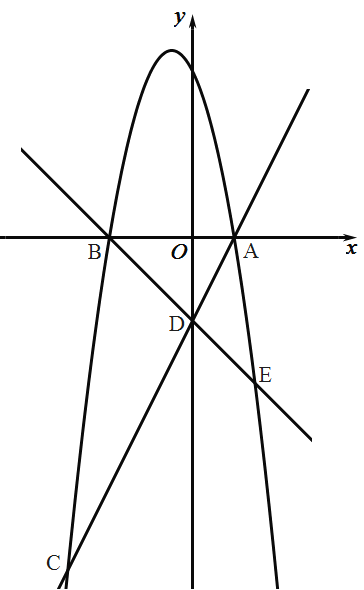
(1)求拋物線的解析式;
(2)點![]() 是直線
是直線![]() 上方拋物線上一動點,求
上方拋物線上一動點,求![]() 面積的最大值;
面積的最大值;
(3)點![]() 是拋物線上一動點,點
是拋物線上一動點,點![]() 是拋物線對稱軸上一動點,請直接寫出以點
是拋物線對稱軸上一動點,請直接寫出以點![]() 為頂點的四邊形是平行四邊形時點
為頂點的四邊形是平行四邊形時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
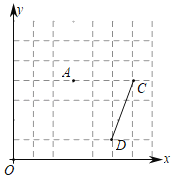
【題目】如圖,在邊長為1的正方形網格中,點A(3,4),⊙A的半徑為![]() .
.
(1)請在網格中畫出⊙A;
(2)請標出⊙A上的三個相鄰的格點B1、B2、B3,連接B1B3,則由![]() 和弦B1B3圍成的弓形面積為 ;
和弦B1B3圍成的弓形面積為 ;
(3)線段CD,點C(6,4)、D(5,1),在⊙A上有一點M,使△CDM的面積最大,請找到此時的點M(保留必要輔助格點N).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB為直徑,AC=5,AB=10,
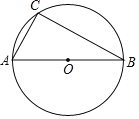
(1)作以AC為底邊的圓內接等腰△ACD;(要求:尺規作圖,不寫作法,保留作圖痕跡)
(2)求弦AC所對的圓周角。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() (
(![]() ,
,![]() ,
,![]() 為常數,且
為常數,且![]() )中的
)中的![]() 與
與![]() 的部分對應值如下表:
的部分對應值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下結論:
①二次函數![]() 有最小值為
有最小值為![]() ;
;
②當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;
的增大而增大;
③二次函數![]() 的圖象與
的圖象與![]() 軸只有一個交點;
軸只有一個交點;
④當![]() 時,
時,![]() .
.
其中正確的結論有( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
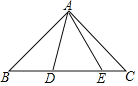
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC,點D,E均在邊BC上,且∠DAE=45°
(1)若BD=2,CE=4,則DE=_____.
(2)若∠AEB=75°,則線段BD與CE的數量關系是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
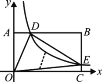
【題目】如圖,在以O為原點的直角坐標系中,矩形OABC的兩邊OC、OA分別在x軸、y軸的正半軸上,反比例函數![]() (x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k的值是( )
(x>0)與AB相交于點D,與BC相交于點E,若BD=3AD,且△ODE的面積是9,則k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com