
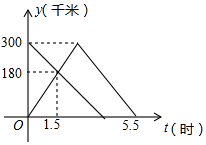
 甲、乙兩車分別從A、B兩地同時出發(fā),甲車勻速前往B地,到達B地立即以另一速度按原路勻速返回到A地;乙車勻速前往A地,設甲、乙兩車距A地的路程為y(千米),甲車行駛的時間為x(時),y與x之間的函數(shù)圖象如圖所示.
甲、乙兩車分別從A、B兩地同時出發(fā),甲車勻速前往B地,到達B地立即以另一速度按原路勻速返回到A地;乙車勻速前往A地,設甲、乙兩車距A地的路程為y(千米),甲車行駛的時間為x(時),y與x之間的函數(shù)圖象如圖所示.分析 (1)根據(jù)函數(shù)圖象中的數(shù)據(jù)可以求得甲車返回A地時的行駛速度;
(2)根據(jù)函數(shù)圖象中的數(shù)據(jù)可以求得在整個行程中,甲車距A地的路程y與行駛時間x之間的函數(shù)關系式;
(3)根據(jù)題意和(1)和(2)的答案可以求得相遇以后,兩車之間的最大距離,本題得以解決.
解答 解:(1)由圖象可得,
甲車從A地到B地的速度為:180÷1.5=120千米/時,
∴甲車從A地到B地的時間為:300÷120=2.5(小時),
∴甲車返回A地時的行駛速度是:300÷(5.5-2.5)=100千米/時,
即甲車返回A地時的行駛速度是100千米/時;
(2)當0≤x≤2.5時,設甲車距A地的路程y與行駛時間x之間的函數(shù)關系式y(tǒng)=kx,
則180=1.5k,得k=120,
即當0≤x≤2.5時,甲車距A地的路程y與行駛時間x之間的函數(shù)關系式是y=120x,
當2.5<x≤5.5時,設甲車距A地的路程y與行駛時間x之間的函數(shù)關系式y(tǒng)=ax+b,
$\left\{\begin{array}{l}{2.5a+b=300}\\{5.5a+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-100}\\{b=550}\end{array}\right.$,
即當2.5<x≤5.5時,設甲車距A地的路程y與行駛時間x之間的函數(shù)關系式y(tǒng)=-100x+550,
由上可得,在整個行程中,甲車距A地的路程y與行駛時間x之間的函數(shù)關系式是:y=$\left\{\begin{array}{l}{120x}&{(0≤x≤2.5)}\\{-100x+550}&{(2.5<x≤5.5)}\end{array}\right.$;
(3)設乙車從B地到A地的函數(shù)解析式為y=mx+n,
則$\left\{\begin{array}{l}{n=300}\\{1.5m+n=180}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-80}\\{n=300}\end{array}\right.$,
即乙車從B地到A地的函數(shù)解析式為y=-80x+300;
當1.5<x≤2.5時,120x-(-80x+300)=200x-300,
當x=2.5時,200x-300取得最大值,此時200x-300=200×2.5-300=200,
將y=0代入y=-80x+300,得x=3.75,
當2.5≤x≤3.75時,(-100x+550)-(-80x+300)=-20x+250,
∴當x=2.5時,-20x+250取得最大值,此時-20x+250=-20×2.5+250=200,
由圖象可知,當3.75≤x≤5.5時,兩車之間的隨x的增大而減小,
由上可得,相遇以后,兩車之間的最大距離是200千米.
點評 本題考查一次函數(shù)的應用,解答本題的關鍵是明確題意,找出所求問題需要的條件,利用數(shù)形結合的思想和函數(shù)的思想解答.


科目:初中數(shù)學 來源: 題型:填空題
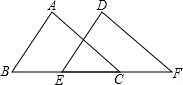 已知,∠ABC=∠DEF,AB=DE,要說明△ABC≌△DEF,若以“AAS”為依據(jù),還要添加的條件為∠ACB=∠F.
已知,∠ABC=∠DEF,AB=DE,要說明△ABC≌△DEF,若以“AAS”為依據(jù),還要添加的條件為∠ACB=∠F.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
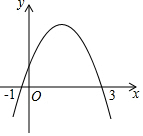 已知拋物線y=ax2+bx+c(a≠0)在平面直角坐標系中的位置如圖,則下列結論中正確的是( )
已知拋物線y=ax2+bx+c(a≠0)在平面直角坐標系中的位置如圖,則下列結論中正確的是( )| A. | a>0 | B. | b<0 | C. | c<0 | D. | a+b+c>0 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com