
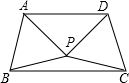
 如圖,△ABP與△CDP是兩個全等的等邊三角形,且PA⊥PD,下列四個結論:
如圖,△ABP與△CDP是兩個全等的等邊三角形,且PA⊥PD,下列四個結論:| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 先求出∠BPC的度數,再根據對稱性得到△BPC為等腰三角形,∠PCB的度數即可求出;再根據題意,有△APD是等腰直角三角形;△PBC是等腰三角形;結合軸對稱圖形的定義與判定,可得四邊形ABCD是軸對稱圖形,進而可得正確結論.
解答 解:∵△ABP≌△CDP,
∴AB=CD,AP=DP,BP=CP.
又∵△ABP與△CDP是兩個等邊三角形,
∴∠PAB=∠PBA=∠APB=60°.
①根據題意,∠BPC=360°-60°×2-90°=150°
∵BP=PC,
∴∠PCB=(180°-150°)÷2=15°,故本選項正確;
②∵∠ABC=60°+15°=75°,
∵AP=DP,
∴∠DAP=45°,
∵∠BAP=60°,
∴∠BAD=∠BAP+∠DAP=60°+45°=105°,
∴∠BAD+∠ABC=105°+75°=180°,
∴AD∥BC,故本選項正確;
③延長CP交于AB于點O.
∠APO=180°-(∠APD+∠CPD)=180°-(90°+60°)=180°-150°=30°,
∵∠PAB=60°,
∴∠AOP=30°+60°=90°,
即PC⊥AB,故本選項正確;
④根據題意可得四邊形ABCD是軸對稱圖形,故本選項正確.
綜上所述,以上四個結論都正確.
故選D.
點評 本題考查全等三角形的判定與性質以及軸對稱圖形的定義與判定的綜合應用,如果一個圖形沿著一條直線對折,兩側的圖形能完全重合,這個圖形就是軸對稱圖形,折痕所在的這條直線叫做對稱軸.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 二次函數y=ax2+bx+c的圖象如圖所示,則一次函數y=ax+b與反比例函數y=$\frac{c}{x}$在同一平面坐標系中的圖象可能是( )
二次函數y=ax2+bx+c的圖象如圖所示,則一次函數y=ax+b與反比例函數y=$\frac{c}{x}$在同一平面坐標系中的圖象可能是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 學生 | 小紅 | 小剛 | 小敏 | 小明 |
| 平均數 | 136 | 136 | 136 | 136 |
| 方差 | 0.32 | 0.18 | 0.24 | 0.27 |
| A. | 小紅 | B. | 小剛 | C. | 小敏 | D. | 小明 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com