
 如圖,在△BCD中,BE平分∠DBC交CD于F,延長BC至G,CE平分∠DCG,且EC、DB的延長線交于A點,若∠A=33°,∠DFE=63°.
如圖,在△BCD中,BE平分∠DBC交CD于F,延長BC至G,CE平分∠DCG,且EC、DB的延長線交于A點,若∠A=33°,∠DFE=63°.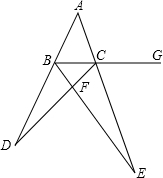 (2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG,
(2)解:∵∠DCG=∠D+∠DBC,CE平分∠DCG, ∠DCG=
∠DCG= (∠D+∠DBC),
(∠D+∠DBC), ∠DBC,
∠DBC, ∠DBC,
∠DBC, ∠DBC=
∠DBC= (∠D+∠DBC),
(∠D+∠DBC), ∠D,
∠D,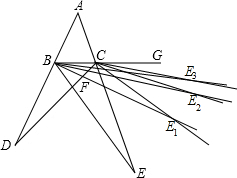 (3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG,
(3)∵∠ECG=∠E+∠EBC,CE1平分∠ECG, ∠ECG=
∠ECG= (∠E+∠EBC).
(∠E+∠EBC). ∠EBC.
∠EBC. ∠EBC,
∠EBC, ∠EBC=
∠EBC= (∠E+∠EBC),
(∠E+∠EBC), ∠E.
∠E. ∠E1,
∠E1, ∠E=
∠E= ∠E,
∠E, ∠E.
∠E. ∠DCG=
∠DCG= (∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+
(∠D+∠DBC),∠ECG=∠E+∠EBC=∠E+ ∠DBC,則∠D=2∠E,再利用上題結(jié)論∠DFE=∠A+∠D+∠E,將已知條件代入,即可求出∠E的度數(shù);
∠DBC,則∠D=2∠E,再利用上題結(jié)論∠DFE=∠A+∠D+∠E,將已知條件代入,即可求出∠E的度數(shù); ∠E,同理得出∠E2=
∠E,同理得出∠E2= ∠E1,則∠E2=
∠E1,則∠E2= ∠E=
∠E= ∠E,由此得出規(guī)律∠En+1=
∠E,由此得出規(guī)律∠En+1= ∠E.
∠E. ∠E,是解題的關(guān)鍵.
∠E,是解題的關(guān)鍵. 

科目:初中數(shù)學(xué) 來源: 題型:
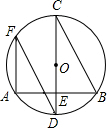 (2013•朝陽區(qū)二模)如圖,在⊙O中,直徑CD⊥弦AB于點E,點F在弧AC上,若∠BCD=32°,則∠AFD的度數(shù)為
(2013•朝陽區(qū)二模)如圖,在⊙O中,直徑CD⊥弦AB于點E,點F在弧AC上,若∠BCD=32°,則∠AFD的度數(shù)為查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,在△BCD中,∠BDC=90°,以BD為斜邊,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC邊上一動點,則DP長的最小值為
如圖,在△BCD中,∠BDC=90°,以BD為斜邊,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC邊上一動點,則DP長的最小值為查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,在△BCD中,BE平分∠DBC交CD于F,延長BC至G,CE平分∠DCG,且EC、DB的延長線交于A點,若∠A=33°,∠DFE=63°.
如圖,在△BCD中,BE平分∠DBC交CD于F,延長BC至G,CE平分∠DCG,且EC、DB的延長線交于A點,若∠A=33°,∠DFE=63°.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
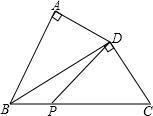 如圖,在△BCD中,∠BDC=90°,以BD為斜邊,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC邊上一動點,則DP長的最小值為________.
如圖,在△BCD中,∠BDC=90°,以BD為斜邊,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC邊上一動點,則DP長的最小值為________.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com