
分析 (1)確定設備更新后第n年的利潤,組成等差數列,求出n年的總利潤,根據當總利潤超過100萬元時可收回投入成本,建立不等式,即可求得結論;
(2)求出當建廠10年時產量最大,年產量Q件與企業建廠年數x的函數關系式為Q=122+14[(x-10)-1]=14x-32,(x>10),根據當Q≥250,可得結論.
解答 解:(1)設至少n年可收回投入成本,則:
設備更新后第一年的產量=122,設備更新后第一年的利潤L1=122×2200
設備更新后第二年的產量=122+14×1,設備更新后第二年的利潤L2=(122+14×1)×2200
…
設備更新后第n年的產量Q=122+14(n-1),設備更新后第n年的利潤Ln=[122+14(n-1)]×2200
∴n年的總利潤L=L1+L2+L3+…+Ln
=2200[122+(122+14)+(122+14×2)+…+122+14(n-1)]
=2200[122n+7n(n-1)]
=2200(7n2+115n)
∵當總利潤超過100萬元時可收回投入成本
∴2200(7n2+115n)≥1000000
∴77n2+1265n-5000≥0
解得n≥3.29或n≤-19.38(舍去)
∵年數取整數,∴n=4
∴至少4年可收回投入成本;
(2)y=-2x2+40x+50=-2(x-10)2+250
∴當建廠10年時產量最大,ymax=250
∴更換設備后,年產量Q件與企業建廠年數x的函數關系式為Q=122+14[(x-10)-1]=14x-32,(x>10)
當Q≥250時有:14x-32≥250,
解得x≥20.14≈20,
∴約建廠20年的時候產量超過設備沒有更換的年產量.
點評 本題考查了二次函數的性質在實際生活中的應用.最大銷售利潤的問題常利函數的增減性來解答,我們首先要吃透題意,確定變量,建立函數模型,然后結合實際選擇最優方案.其中要注意應該在自變量的取值范圍內求最大值(或最小值).


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3500(1+x)=4200 | B. | 3500(1-x)+3500(1-x)2=4200 | ||
| C. | 3500(1-x)=4200 | D. | 3500(1-x)2=4200 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
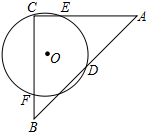 如圖,AC⊥BC,AC=BC,點D是AB中點,過C、D的⊙O交AC、BC分別于E、F.若⊙O的半徑為$\sqrt{3}$,AC=2+2$\sqrt{2}$,則△CEF的面積為( )
如圖,AC⊥BC,AC=BC,點D是AB中點,過C、D的⊙O交AC、BC分別于E、F.若⊙O的半徑為$\sqrt{3}$,AC=2+2$\sqrt{2}$,則△CEF的面積為( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com