
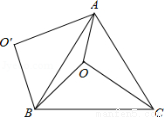
如圖,O是正△ABC內一點,OA=3,OB=4,OC=5,將線段BO以點B為旋轉中心逆時針旋轉60°得到線段BO′,下列結論:①△BO′A可以由△BOC繞點B逆時針旋轉60°得到;②點O與O′的距離為4;③∠AOB=150°;④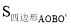 =6+3
=6+3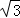 ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+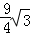 .其中正確的結論是( )
.其中正確的結論是( )
A.①②③⑤ B.①②③④ C.②③④⑤ D.①②④⑤
A.
【解析】
試題分析:證明△BO′A≌△BOC,又∠OBO′=60°,所以△BO′A可以由△BOC繞點B逆時針旋轉60°得到,故結論①正確;由△OBO′是等邊三角形,可知結論②正確;在△AOO′中,三邊長為3,4,5,這是一組勾股數,故△AOO′是直角三角形;進而求得∠AOB=150°,故結論③正確;S四邊形AOBO′=S△AOO′+S△OBO′=6+4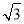 ,故結論④錯誤;如圖②,將△AOB繞點A逆時針旋轉60°,使得AB與AC重合,點O旋轉至O″點.利用旋轉變換構造等邊三角形與直角三角形,將S△AOC+S△AOB轉化為S△COO″+S△AOO″,計算可得結論⑤正確.
,故結論④錯誤;如圖②,將△AOB繞點A逆時針旋轉60°,使得AB與AC重合,點O旋轉至O″點.利用旋轉變換構造等邊三角形與直角三角形,將S△AOC+S△AOB轉化為S△COO″+S△AOO″,計算可得結論⑤正確.
試題解析:由題意可知,∠1+∠2=∠3+∠2=60°,∴∠1=∠3,
又∵OB=O′B,AB=BC,
∴△BO′A≌△BOC,又∵∠OBO′=60°,
∴△BO′A可以由△BOC繞點B逆時針旋轉60°得到,
故結論①正確;
如圖①,連接OO′,
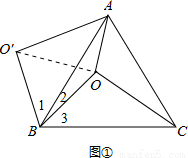
∵OB=O′B,且∠OBO′=60°,
∴△OBO′是等邊三角形,
∴OO′=OB=4.
故結論②正確;
∵△BO′A≌△BOC,
∴O′A=5.
在△AOO′中,三邊長為3,4,5,這是一組勾股數,
∴△AOO′是直角三角形,∠AOO′=90°,
∴∠AOB=∠AOO′+∠BOO′=90°+60°=150°,
故結論③正確;
S四邊形AOBO′=S△AOO′+S△OBO′=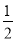 ×3×4+
×3×4+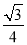 ×42=6+4
×42=6+4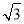 ,
,
故結論④錯誤;
如圖②所示,
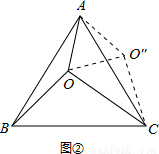
將△AOB繞點A逆時針旋轉60°,使得AB與AC重合,點O旋轉至O″點.
易知△AOO″是邊長為3的等邊三角形,△COO″是邊長為3、4、5的直角三角形,
則S△AOC+S△AOB=S四邊形AOCO″=S△COO″+S△AOO″=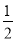 ×3×4+
×3×4+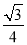 ×32=6+
×32=6+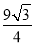 ,
,
故結論⑤正確.
綜上所述,正確的結論為:①②③⑤.
故選A.
考點:1.旋轉的性質;2.全等三角形的判定與性質;3.等邊三角形的判定與性質;4.勾股定理的逆定理.


科目:初中數學 來源:2014-2015學年江蘇省無錫市錫山區九年級上學期期中考試數學試卷(解析版) 題型:填空題
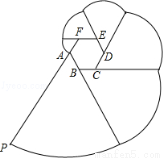
如圖,正六邊形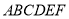 是邊長為
是邊長為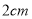 的螺母,點
的螺母,點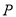 是
是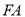 延長線上的點,在
延長線上的點,在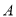 、
、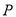 之間拉一條長為
之間拉一條長為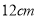 的無伸縮性細線,一端固定在點
的無伸縮性細線,一端固定在點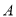 ,握住另一端點
,握住另一端點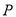 拉直細線,把它全部緊緊纏繞在螺母上(纏繞時螺母不動),則點
拉直細線,把它全部緊緊纏繞在螺母上(纏繞時螺母不動),則點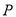 運動的路徑長為___________.
運動的路徑長為___________.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省孝感市孝南區三校九年級12月月考數學試卷(解析版) 題型:解答題
如圖,在平面直角坐標系中,已知點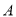 坐標為(2,4),直線
坐標為(2,4),直線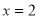 與
與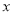 軸相交于點
軸相交于點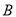 ,連結
,連結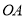 ,拋物線
,拋物線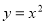 從點
從點 沿
沿 方向平移,與直線
方向平移,與直線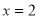 交于點
交于點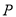 ,頂點
,頂點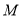 到
到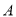 點時停止移動.
點時停止移動.
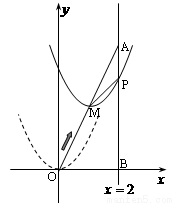
(1)求線段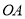 所在直線的函數解析式;
所在直線的函數解析式;
(2)設拋物線頂點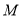 的橫坐標為
的橫坐標為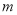 .
.
①用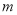 的代數式表示點
的代數式表示點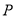 的坐標;
的坐標;
②當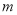 為何值時,線段
為何值時,線段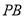 最短;
最短;
(3)當線段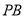 最短時,相應的拋物線上是否存在點
最短時,相應的拋物線上是否存在點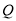 ,使△
,使△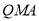 的面積與△
的面積與△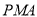 的面積相等,若存在,請直接寫出點
的面積相等,若存在,請直接寫出點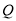 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省孝感市孝南區三校九年級12月月考數學試卷(解析版) 題型:填空題
如圖所示:下列正多邊形都滿足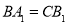 ,在正三角形中,我們可推得:
,在正三角形中,我們可推得: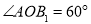 ;在正方形中,可推得:
;在正方形中,可推得: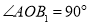 ;在正五邊形中,可推得:
;在正五邊形中,可推得: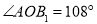 ,依此類推在正
,依此類推在正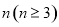 邊形中,
邊形中,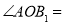
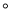 .
.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年湖北省孝感市孝南區三校九年級12月月考數學試卷(解析版) 題型:選擇題
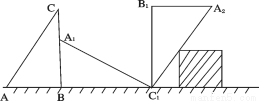
如圖,張三同學把一個直角邊長分別為3cm,4cm的直角三角形硬紙板,在桌面上翻滾(順時針方向),頂點A的位置變化為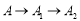 ,其中第二次翻滾時被桌面上一小木塊擋住,使紙板一邊
,其中第二次翻滾時被桌面上一小木塊擋住,使紙板一邊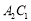 與桌面所成的角恰好等于
與桌面所成的角恰好等于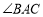 ,則
,則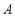 翻滾到
翻滾到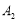 位置時共走過的路程為( )
位置時共走過的路程為( )
A.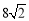 cm B.
cm B.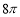 cm C.
cm C.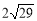 cm D.
cm D. 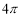 cm
cm
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省陸豐市九年級上學期期末考試數學試卷(解析版) 題型:解答題
如圖所示,已知OABC是-張放在平面直角坐標系中的矩形紙片,O為坐標原點,點A在x軸上,點C在y軸上,且0A=15,0C=9,在邊AB上選取-點D,將△AOD沿OD翻折,使點A落在BC邊上,記為點E.
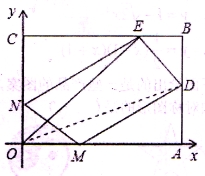
(1)求DE所在直線的解析式;
(2)設點P在x軸上,以點O、E、P為頂點的三角形是等腰三角形,問這樣的點P有幾個?并求出所有滿足條件的點P的坐標;
(3)在x軸、y軸上是否分別存在點M、N,使四邊形MNED的周長最小?如果存在,求出周長的最小值;如果不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年廣東省陸豐市九年級上學期期末考試數學試卷(解析版) 題型:選擇題
二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:(1)c<0 (2)b>0(3)4a+2b+c>0 其中正確的有( )
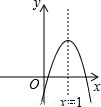
A.1個 B.2個 C.3個 D.0個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省廣安市白廟督導區七年級10月月考數學試卷(解析版) 題型:填空題
數軸上表示數﹣6與﹣20的兩點之間的距離是 _________ 。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com