
分析 (1)利用非負(fù)數(shù)的性質(zhì)可求得a、b的值,根據(jù)三角形三邊關(guān)系可求得c的范圍;
(2)分腰長為3或4兩種情況進(jìn)行計(jì)算;
(3)分這兩個(gè)內(nèi)角一個(gè)為頂角和兩個(gè)都是底角三種情況,結(jié)合三角形內(nèi)角和定理可求得x,可得出三個(gè)角的度數(shù).
解答 解:(1)∵|a-3|+(b-4)2=0,
∴a=3 b=4,
∵b-a<c<b+a,
∴1<c<7;
(2)當(dāng)腰長為3時(shí),此時(shí)三角形的三邊為3、3、4,滿足三角形三邊關(guān)系,周長為10;
當(dāng)腰長為4時(shí),此時(shí)三角形的三邊長為4、4、3,滿足三角形三邊關(guān)系,周長為11;
綜上可知等腰三角形的周長為10或11;
(3)當(dāng)?shù)捉菫閤°、頂角為(2x-20)°時(shí),則根據(jù)三角形內(nèi)角和為180°可得
x+x+2x-20=180,
解得x=50,
此時(shí)三個(gè)內(nèi)角分別為50°、50°、80°;
當(dāng)頂角為x°、底角為(2x-20)°時(shí),則根據(jù)三角形內(nèi)角和為180°可得
x+2x-20+2x-20=180,
解得x=44,
此時(shí)三個(gè)內(nèi)角分別為44°、68°、68°;
當(dāng)?shù)捉菫閤°、(2x-20)°時(shí),則等腰三角形性質(zhì)可得
x=2x-20,
解得x=20,
此時(shí)三個(gè)內(nèi)角分別為20°、20°、140°;
綜上可知三角形三個(gè)內(nèi)角為50度、50度、80度或44度、68度、68度或20度、20度、140度.
點(diǎn)評(píng) 本題主要考查等腰三角形的性質(zhì),掌握等腰三角形的兩腰相等、兩底角相等是解題的關(guān)鍵.


 名師伴你成長課時(shí)同步學(xué)練測系列答案
名師伴你成長課時(shí)同步學(xué)練測系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 線段比直線長 | |
| B. | 過同一平面內(nèi)的兩點(diǎn),可以作三條直線 | |
| C. | 一條射線有兩個(gè)端點(diǎn) | |
| D. | 兩點(diǎn)之間的所有連線中,線段最短 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
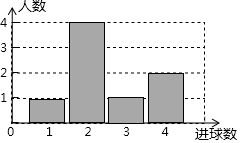 體育課上,老師為了解女學(xué)生定點(diǎn)投籃的情況,隨機(jī)抽取8名女生進(jìn)行每人4次定點(diǎn)投籃的測試,進(jìn)球數(shù)的統(tǒng)計(jì)如圖所示.
體育課上,老師為了解女學(xué)生定點(diǎn)投籃的情況,隨機(jī)抽取8名女生進(jìn)行每人4次定點(diǎn)投籃的測試,進(jìn)球數(shù)的統(tǒng)計(jì)如圖所示.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=3x-1 | B. | y=x3-2x-3 | C. | y=(x+1)2-x2 | D. | y=3x2-1 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com