
分析 (1)由A打第一場,再從其余三人中隨機選取一人打第一場,求出恰好選中B的概率即可;
(2)畫樹狀圖得出所有等可能的情況數,找出B和D伸“手心”或“手背”恰好相同的情況數,即可求出所求的概率.
解答 解:(1)∵確定A同學打第一場,
∴再從B、C、D隨機選取一人打第一場,恰好選中B同學的概率為$\frac{1}{3}$;
(2)畫樹狀圖如下: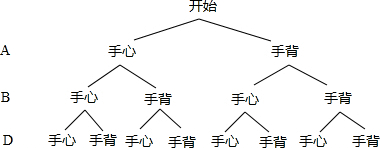
所有等可能的情況有8種,其中B同學和D同學伸“手心”或“手背”恰好相同且與A不同的結果有2個,
則B同學和D同學打第一場的概率為$\frac{2}{8}$=$\frac{1}{4}$.
點評 此題考查了概率公式、列表法與樹狀圖法求概率的知識.注意列表法與樹狀圖法可以不重復不遺漏的列出所有可能的結果,列表法適合于兩步完成的事件;樹狀圖法適合兩步或兩步以上完成的事件.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:填空題
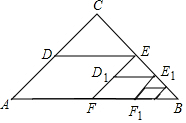 如圖,△ABC中,∠C=90°,AC=BC=2,取BC邊中點E,作ED∥AB,EF∥AC,得到四邊形EDAF,它的面積記作S1;取BE中點E1,作E1D1∥FB,E1F1∥EF,得到四邊形E1D1FF1,它的面積記作S2,照此規律作下去,則S1=1,S2017=$\frac{1}{{4}^{2016}}$.
如圖,△ABC中,∠C=90°,AC=BC=2,取BC邊中點E,作ED∥AB,EF∥AC,得到四邊形EDAF,它的面積記作S1;取BE中點E1,作E1D1∥FB,E1F1∥EF,得到四邊形E1D1FF1,它的面積記作S2,照此規律作下去,則S1=1,S2017=$\frac{1}{{4}^{2016}}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 至少有1個球是白球 | B. | 至少有1個球是黑球 | ||
| C. | 至少有2個球是黑球 | D. | 至少有2個球是白球 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
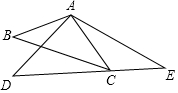 如圖,△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,則∠BCD=20度.
如圖,△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,則∠BCD=20度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com