
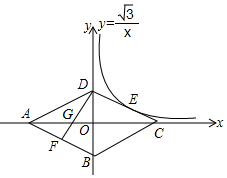
 已知如圖,菱形ABCD的四個頂點均在坐標軸上,對角線AC、BD交于原點O,DF⊥AB交AC于點G,反比例函數y=$\frac{\sqrt{3}}{x}$(x>0)經過線段DC的中點E,若BD=4,則AG的長為( )
已知如圖,菱形ABCD的四個頂點均在坐標軸上,對角線AC、BD交于原點O,DF⊥AB交AC于點G,反比例函數y=$\frac{\sqrt{3}}{x}$(x>0)經過線段DC的中點E,若BD=4,則AG的長為( )| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\sqrt{3}$+2 | C. | 2$\sqrt{3}$+1 | D. | $\frac{3\sqrt{3}}{2}$+1 |
分析 過E作y軸和x的垂線EM,EN,證明四邊形MENO是矩形,設E(b,a),根據反比例函數圖象上點的坐標特點可得ab=$\sqrt{3}$,進而可計算出CO長,根據三角函數可得∠DCO=30°,再根據菱形的性質可得∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2$\sqrt{3}$,然后利用勾股定理計算出DG長,進而可得AG長.
解答 解:過E作y軸和x的垂線EM,EN,
設E(b,a),
∵反比例函數y=$\frac{\sqrt{3}}{x}$(x>0)經過點E,
∴ab=$\sqrt{3}$,
∵四邊形ABCD是菱形,
∴BD⊥AC,DO=$\frac{1}{2}$BD=2,
∵EN⊥x,EM⊥y,
∴四邊形MENO是矩形,
∴ME∥x,EN∥y,
∵E為CD的中點,
∴DO•CO=4$\sqrt{3}$,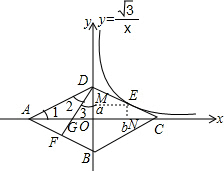
∴CO=2$\sqrt{3}$,
∴tan∠DCO=$\frac{DO}{CO}$=$\frac{\sqrt{3}}{3}$,
∴∠DCO=30°,
∵四邊形ABCD是菱形,
∴∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2$\sqrt{3}$,
∵DF⊥AB,
∴∠2=30°,
∴DG=AG,
設DG=r,則AG=r,GO=2$\sqrt{3}$-r,
∵AD=AB,∠DAB=60°,
∴△ABD是等邊三角形,
∴∠ADB=60°,
∴∠3=30°,
在Rt△DOG中,DG2=GO2+DO2,
∴r2=(2$\sqrt{3}$-r)2+22,
解得:r=$\frac{4\sqrt{3}}{3}$,
∴AG=$\frac{4\sqrt{3}}{3}$,
故選:A.
點評 此題主要考查了反比例函數和菱形的綜合運用,關鍵是掌握菱形的性質:菱形對角線互相垂直平分,且平分每一組對角,反比例函數圖象上的點橫縱坐標之積=k.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
| 里 程 | 收費(元) |
| 3km以下(含3km) | 5.00 |
| 3km以上,每增加1km | 1.20 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,是李明同學在求陰影部分的面積時,列出的4個式子,其中錯誤的是( )
如圖,是李明同學在求陰影部分的面積時,列出的4個式子,其中錯誤的是( )| A. | ab+(c-a)a | B. | ac+(b-a)a | C. | ab+ac-a2 | D. | bc+ac-a2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=3,n=-2 | B. | m=3,n=2 | C. | m=-3,n=-2 | D. | m=-3,n=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com