
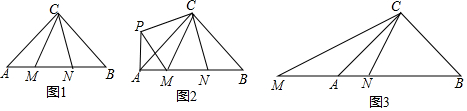
分析 (1)將△BCN繞點C按順時針方向旋轉90°得△ACP,連接MP,根據SAS證得△MCP≌△MCN,得出MP=MN,再根據∠PAM=∠CAP+∠CAB=90°,運用勾股定理得出Rt△APM中,PM2=AM2+AP2,進而得到MN2=AM2+BM2;
(2)將△BCN繞點C按順時針方向旋轉90°得△ACP,連接MP,得出∠PCN=∠ACB=90°,PC=NC,AP=BN,∠CAP=∠B=45°,根據SAS證得△MCP△MCN,進而得出MP=MN,再根據∠PAB=∠CAP+∠CAB=90°,得到∠PAM=90°,在Rt△APM中,根據勾股定理得到PM2=AM2+AP2,進而得出MN2=AM2+BM2..
解答 解:(1)①如圖2,將△BCN繞點C按順時針方向旋轉90°得△ACP,連接MP,則
∠BCN=∠ACP,
∵在△ABC中,∠ACB=90°,∠MCN=45°,
∴∠ACM+∠BCN=45°,
∴∠ACP+∠ACM=45°,
∴∠PCM=∠NCM;
②證明:由旋轉可得△CAP≌△CBN,
∴AP=BN,PC=NC,∠CAP=∠B=45°,
在△MCP和△MCN中,
$\left\{\begin{array}{l}{PC=NC}\\{∠PCM=∠NCM}\\{CM=CM}\end{array}\right.$,
∴△MCP≌△MCN(SAS),
∴MP=MN,
∵∠PAM=∠CAP+∠CAB=90°,
∴Rt△APM中,PM2=AM2+AP2,
∴MN2=AM2+BM2;
(2)MN2=AM2+BM2,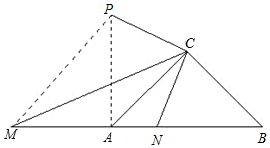
理由:如圖,將△BCN繞點C按順時針方向旋轉90°得△ACP,連接MP,則
∠PCN=∠ACB=90°,PC=NC,AP=BN,∠CAP=∠B=45°,
∵∠MCN=45°,
∴∠PCM=90°-45°=45°,
∴∠PCM=∠NCP,
在△MCP和△MCN中,
$\left\{\begin{array}{l}{PC=NC}\\{∠PCM=∠NCM}\\{CM=CM}\end{array}\right.$,
∴△MCP△MCN(SAS),
∴MP=MN,
∵∠PAB=∠CAP+∠CAB=90°,
∴∠PAM=90°,
∴Rt△APM中,PM2=AM2+AP2,
∴MN2=AM2+BM2.
點評 此題屬于三角形綜合題,主要考查了旋轉的性質,等腰直角三角形的性質,勾股定理及全等三角形的判定與性質的綜合應用.解題的關鍵是運用:旋轉前、后的圖形全等.解題時注意:等腰直角三角形是一種特殊的三角形,具有所有三角形的性質,還具備等腰三角形和直角三角形的所有性質.


科目:初中數學 來源: 題型:填空題
 如圖,△ABC、△ADE均為等邊三角形,AD平分∠BAC交BC于D,DE交AB于F,則下列結論:①AD⊥BC;②EF=FD; ③BE=BD,其中正確的有①②③(填序號).
如圖,△ABC、△ADE均為等邊三角形,AD平分∠BAC交BC于D,DE交AB于F,則下列結論:①AD⊥BC;②EF=FD; ③BE=BD,其中正確的有①②③(填序號).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 解不等式(組),并把題(2)的解在數軸上表示出來..
解不等式(組),并把題(2)的解在數軸上表示出來..查看答案和解析>>
科目:初中數學 來源: 題型:解答題
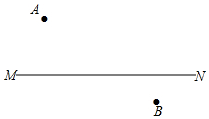 如圖,在直線MN的異側有A、B兩點,按要求畫圖取點,并寫出畫圖的依據.
如圖,在直線MN的異側有A、B兩點,按要求畫圖取點,并寫出畫圖的依據.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
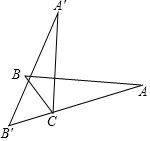 如圖,在△ABC中,∠A:∠B:∠ACB=2:5:11,若將△ACB繞點C逆時針旋轉,使旋轉前后的△A′B′C中的頂點B′在原三角形的邊AC的延長線上,求∠BCA′的度數.
如圖,在△ABC中,∠A:∠B:∠ACB=2:5:11,若將△ACB繞點C逆時針旋轉,使旋轉前后的△A′B′C中的頂點B′在原三角形的邊AC的延長線上,求∠BCA′的度數.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com