
【題目】若關于![]() 的二次函數
的二次函數![]() (
(![]() 為常數)與
為常數)與![]() 軸交于兩個不同的點
軸交于兩個不同的點![]() 、
、![]() ,與
,與![]() 軸交于點
軸交于點![]() ,其圖象的頂點為點
,其圖象的頂點為點![]() 是坐標原點.
是坐標原點.
(1)若![]() 、
、![]() 、
、![]() ,求此二次函數的解析式并寫出二次函數的對稱軸;
,求此二次函數的解析式并寫出二次函數的對稱軸;
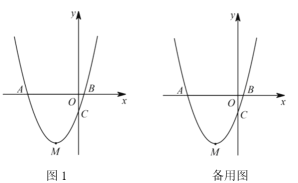
(2)如圖1,若![]() ,
,![]() ,
,![]() 為直角三角形,
為直角三角形,![]() 是以
是以![]() 的等邊三角形,試確定
的等邊三角形,試確定![]() 的值;
的值;
(3)設![]() 為正整數,且
為正整數,且![]() ,
,![]() ,
,![]() 為任意常數,令
為任意常數,令![]() ,
,![]() ,如果對于一切實數
,如果對于一切實數![]() ,
,![]() 始終成立,求
始終成立,求![]() 的值.
的值.
【答案】(1)![]() ,對稱軸
,對稱軸![]() ;(2)
;(2)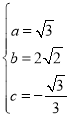 ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)函數的表達式為:y=a(x+2)(x-4)=a(x2-2x-8),即可求解;
(2)設![]() ,
,![]() ,
,![]() ,由
,由![]() ,得到
,得到![]() ,結合一元二次方程根與系數的關系,得到
,結合一元二次方程根與系數的關系,得到![]() ;由
;由![]() 為邊長2的等邊三角形,則
為邊長2的等邊三角形,則![]() ,得到
,得到![]() ;由
;由![]() ,得到
,得到![]() ,聯立方程組,即可求出a、b、c的值.
,聯立方程組,即可求出a、b、c的值.
(3)先表示出解析式,求出點A、B的橫坐標,得到AB=x2-x1=|mt+3|≥|2t+n|,對于一切實數t,上式都成立,則必然存在|mt+3|=|2t+n|,結合一元二次方程根的判別式即可求解.
解:(1)設函數的表達式為:y=a(x+2)(x-4)=a(x2-2x-8),
把點C代入,則-8a=3,
解得:![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴對稱軸![]() ;
;
(2)設![]() ,
,![]() ,
,![]() ,
,
∵![]() 為直角三角形,且
為直角三角形,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,
,
則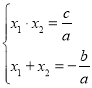 ,
,
∴![]() ,
,
∴![]() ①;
①;
又∵![]() 為邊長2的等邊三角形,
為邊長2的等邊三角形,
∴拋物線頂點坐標中縱坐標為![]() ,且
,且![]() .
.
∴![]() ,
,
∴![]() ②;
②;
又∵![]()
∴![]() ③
③
由①②③得: ,
,
解得: ;
;
(3)根據題意,解析式:![]() .
.
令![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴AB=![]() ;
;
∴![]() (兩邊平方),
(兩邊平方),
∴![]() ,
,
∴![]() ,
,
∴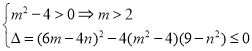 恒成立.
恒成立.
∴![]() ,
,
∴![]() 且
且![]() 為正整數
為正整數
∴![]() 或
或![]() .
.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數學 來源: 題型:
【題目】圖①,圖②均是![]() 的正方形網格,每個小正方形的邊長均為1,每個小正方形的頂點叫做格點.線段
的正方形網格,每個小正方形的邊長均為1,每個小正方形的頂點叫做格點.線段![]() 的端點都在格點上,僅用無刻度的直尺完成如下作圖,保留作圖痕跡.
的端點都在格點上,僅用無刻度的直尺完成如下作圖,保留作圖痕跡.
(1)在圖①中畫一個鈍角![]() ,且點
,且點![]() 在格點上,使它有一邊與該邊上的高線長度相等;
在格點上,使它有一邊與該邊上的高線長度相等;
(2)在圖②中畫一個五邊形![]() ,使其是軸對稱圖形,且
,使其是軸對稱圖形,且![]() ,點
,點![]() 、
、![]() 、
、![]() 在格點上.
在格點上.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中秋節是我國傳統佳節,圓圓同學帶了4個月餅(除餡不同外,其它均相同),其中有兩個火腿餡月餅、一個蛋黃餡和一個棗泥餡月餅.
(1)請你根據上述描述,寫出一個不可能事件.
(2)圓圓準備從中任意拿出兩個送給她的好朋友月月.
①用樹狀圖或列表的方法列出圓圓拿到兩個月餅的所有可能結果;
②請你計算圓圓拿到的兩個月餅都是火腿餡的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在長方形ABCD中,![]() ,
,![]() ,點P從A開始沿邊AB向終點B以
,點P從A開始沿邊AB向終點B以![]() 的速度移動,與此同時,點Q從點B開始沿邊BC向終點C以
的速度移動,與此同時,點Q從點B開始沿邊BC向終點C以![]() 的速度移動,如果P,Q分別從A,B同時出發,當點Q運動到點C時,兩點停止運動
的速度移動,如果P,Q分別從A,B同時出發,當點Q運動到點C時,兩點停止運動![]() 設運動時間為t秒.
設運動時間為t秒.
![]() 填空:
填空:![]() ________,
________,![]() ________
________![]() 用含t的代數式表示
用含t的代數式表示![]() :
:
![]() 當t為何值時,PQ的長度等于5cm?
當t為何值時,PQ的長度等于5cm?
![]() 是否存在t的值,使得五邊形APQCD的面積等于
是否存在t的值,使得五邊形APQCD的面積等于![]() ?若存在,請求出此時t的值;若不存在,請說明理由.
?若存在,請求出此時t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著生活水平的提高,人們越來越注重營養健康,有一種有機水果![]() 在市場上特別受歡迎,某大型超市以10元/千克的價格在產地收購了6000千克
在市場上特別受歡迎,某大型超市以10元/千克的價格在產地收購了6000千克![]() 水果,立即將其冷藏,請根據下列信息解決問題:
水果,立即將其冷藏,請根據下列信息解決問題:
①水果![]() 的市場價每天每千克上漲0.1元;
的市場價每天每千克上漲0.1元;
②平均每天有10千克的該水果損壞,不能出售;
③每天的冷藏費用為300元;
④該水果最多保存110天;
(1)若將這批![]() 水果存放
水果存放![]() 天后一次性出售,則
天后一次性出售,則![]() 天后這批水果的銷售單價為 元;
天后這批水果的銷售單價為 元;
(2)將這批![]() 水果存放多少天后一次性出售所得利潤為9600元?
水果存放多少天后一次性出售所得利潤為9600元?
(3)將這批![]() 水果存放多少天后一次性出售可獲得最大利潤?最大利潤是多少?
水果存放多少天后一次性出售可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
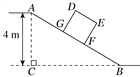
【題目】如圖,某倉儲中心有一斜坡AB,其坡比為i=1∶2,頂部A處的高AC為4 m,B,C在同一水平面上.
(1)求斜坡AB的水平寬度BC;
(2)矩形DEFG為長方形貨柜的側面圖,其中DE=2.5 m,EF=2 m.將貨柜沿斜坡向上運送,當BF=3.5 m時,求點D離地面的高.(![]() ≈2.236,結果精確到0.1 m)
≈2.236,結果精確到0.1 m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初中生的視力狀況受到社會的廣泛關注,某市有關部門對全市3萬名初中生的視力狀況進行了一次抽樣調查,下圖是利用所得數據繪制的頻數分布直方圖,根據圖中所提供的信息回答下列問題:
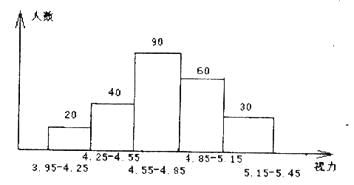
(1)本次調查共抽測了多少名學生?
(2)在這個問題中的樣本指什么?
(3)如果視力在4.9-5.1(含4.9和5.1)均屬正常,那么全市有多少名初中生視力正常?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,對角線AC與BD相交于點O,在DC的延長線上取一點E,連接OE交BC于點F.已知AB=4,BC=6,CE=2,則CF的長等于( )
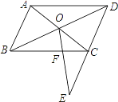
A. 1 B. 1.5 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知直線y=﹣2x+4與兩坐標軸分別交于點A、B,點C為線段OA上一動點,連接BC,作BC的中垂線分別交OB、AB交于點D、E.
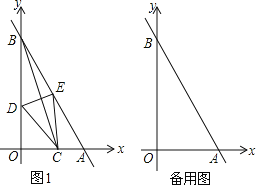
(l)當點C與點O重合時,DE= ;
(2)當CE∥OB時,證明此時四邊形BDCE為菱形;
(3)在點C的運動過程中,直接寫出OD的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com