【題目】初中生的視力狀況受到社會的廣泛關注，某市有關部門對全市3萬名初中生的視力狀況進行了一次抽樣調查，下圖是利用所得數據繪制的頻數分布直方圖，根據圖中所提供的信息回答下列問題：
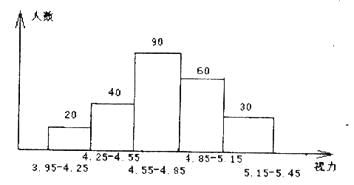
（1）本次調查共抽測了多少名學生？
（2）在這個問題中的樣本指什么？
（3）如果視力在4.9-5.1（含4.9和5.1）均屬正常，那么全市有多少名初中生視力正常？
科目：初中數學 來源： 題型：
【題目】如圖，已知AD∥BC，點E為CD上一點，AE，BE分別平分∠DAB，∠CBA．
（1）求證：AE⊥BE；
（2）求證：DE=CE；
（3）若AE=4，BE=6，求四邊形ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A（3，0），B（0，3），過點B畫y軸的垂線l，點C在線段AB上，連結OC并延長交直線l于點D，過點C畫CE⊥OC交直線l于點E．
（1）求∠OBA的度數，并直接寫出直線AB的解析式；
（2）若點C的橫坐標為2，求BE的長；
（3）當BE＝1時，求點C的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若關于
的二次函數
（
為常數）與軸交于兩個不同的點
、
，與
軸交于點
，其圖象的頂點為點
是坐標原點．
（1）若
、
、
，求此二次函數的解析式并寫出二次函數的對稱軸；
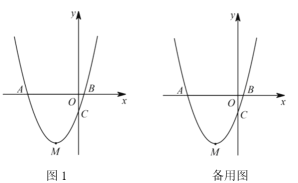
（2）如圖1，若
，
，
為直角三角形，
是以
的等邊三角形，試確定的值；
（3）設
為正整數，且
，
，
為任意常數，令
，
，如果對于一切實數，
始終成立，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
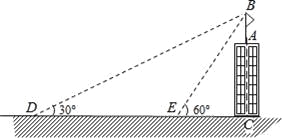
【題目】如圖，某建筑物AC頂部有一旗桿AB，且點A，B，C在同一條直線上，小明在地面D處觀測旗桿頂端B的仰角為30°，然后他正對建筑物的方向前進了20米到達地面的E處，又測得旗桿頂端B的仰角為60°，已知建筑物的高度AC=12m，求旗桿AB的高度（結果精確到0.1米）．參考數據：
≈1.73，
≈1.41．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】請閱讀下列材料，并完成相應的任務：
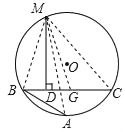
阿基米德是有史以來最偉大的數學家之一，阿基米德的折弦定理是其推導出來的重要定理之一．阿基米德折弦定理：如圖，AB和BC是⊙O的兩條弦（即折線ABC是⊙O的一條折弦），BC＞AB，M是弧ABC的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD＝AB+BD．下面是運用“截長法”證明CD＝AB+BD的部分證明過程．
證明：如圖，在CB上截取CG＝AB，連接MA，MB，MC和MG．
∵M是弧ABC的中點，
∴MA＝MC．
…
請按照上面的證明思路，寫出該證明的剩余部分．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠A=∠B，AE=BE，點D在AC邊上，∠1=∠2，AE和BD相交于點O．
（1）求證：△AEC≌△BED；
（2）若∠1=42°，求∠BDE的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某甜品店計劃訂購一種鮮奶，根據以往的銷售經驗，當天的需求量與當天的最高氣溫T有關，現將去年六月份（按30天計算）的有關情況統計如下：（最高氣溫與需求量統計表）
最高氣溫（單位：攝氏度） | 需求量（單位：杯） |
T<25 | 250 |
| 300 |
| 400 |
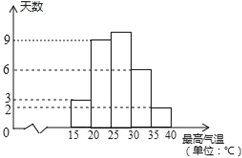
（1）求去年六月份最高氣溫不高于30℃的天數．
（2）若以最高氣溫位于各區間的頻率估計最高氣溫位于該區間的概率，求去年六月份這種鮮奶一天的需求量不超過250杯的概率．
（3）若今年六月份每天的進貨量均為350杯，每杯的進價為5元，售價為10元，未售出的這種鮮奶廠家以1元的價格收回銷毀，假設今年與去年的情況大致一樣，若今年六月份某天的最高氣溫T滿足大于等于25℃小于30℃ ，試估計這一天銷售這種鮮奶所獲得的利潤為多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中考英語聽力測試期間T需要杜絕考點周圍的噪音．如圖，點A是某市一中考考點，在位于考點南偏西15°方向距離500米的C點處有一消防隊．在聽力考試期間，消防隊突然接到報警電話，消防車需沿北偏東75°方向的公路CF前往救援．已知消防車的警報聲傳播半徑為400米，若消防車的警報聲對聽力測試造成影響，則消防車必須改道行駛．試問：消防車是否需要改道行駛？
說明理由．（
≈1.732）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
