Question

14．在平面直角坐標系xOy中，拋物線$y=\frac{1}{2}{x^2}+bx+c$經(jīng)過點A（0，2）和B（1，$\frac{3}{2}$）．
（1）求該拋物線的表達式；
（2）已知點C與點A關(guān)于此拋物線的對稱軸對稱，點D在拋物線上，且點D的橫坐標為4，求點C與點D的坐標；
（3）在（2）的條件下，將拋物線在點A，D之間的部分（含點A，D）記為圖象G，如果圖象G向下平移t（t＞0）個單位后與直線BC只有一個公共點，求t的取值范圍．

Answer 1

分析 （1）把A點和B點坐標代入$y=\frac{1}{2}{x^2}+bx+c$得到關(guān)于b、c的方程組，然后解方程組求出b、c即可得到拋物線解析式；
（2）利用配方法得到y(tǒng)=$\frac{1}{2}$（x-1）²+$\frac{3}{2}$，則拋物線的對稱軸為直線x=1，利用點C與點A關(guān)于直線x=1對稱得到C點坐標為（2，2）；然后利用二次函數(shù)圖象上點的坐標特征求D點坐標；
（3）畫出拋物線，如圖，先利用待定系數(shù)法求出直線BC的解析式為y=$\frac{1}{2}$x+1，再利用平移的性質(zhì)得到圖象G向下平移1個單位時，點A在直線BC上；圖象G向下平移3個單位時，點D在直線BC上，由于圖象G向下平移t（t＞0）個單位后與直線BC只有一個公共點，所以1＜t≤3．

解答 解：（1）把A（0，2）和B（1，$\frac{3}{2}$）代入$y=\frac{1}{2}{x^2}+bx+c$得$\left\{\begin{array}{l}{c=2}\\{\frac{1}{2}+b+c=\frac{3}{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{b=-1}\\{c=2}\end{array}\right.$，
所以拋物線解析式為y=$\frac{1}{2}$x²-x+2；
（2）∵y=$\frac{1}{2}$x²-x+2=$\frac{1}{2}$（x-1）²+$\frac{3}{2}$，
∴拋物線的對稱軸為直線x=1，
∵點C與點A關(guān)于此拋物線的對稱軸對稱，
∴C點坐標為（2，2）；
當x=4時，y=$\frac{1}{2}$x²-x+2=8-4+2=6，
∴D點坐標為（4，6）；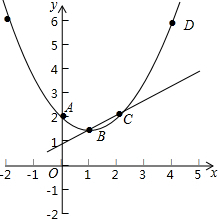
（3）如圖，
設直線BC的解析式為y=mx+n，
把B（1，$\frac{3}{2}$），C（2，2）代入得$\left\{\begin{array}{l}{m+n=\frac{3}{2}}\\{2m+n=2}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=1}\end{array}\right.$，
∴直線BC的解析式為y=$\frac{1}{2}$x+1，
當x=0時，y=$\frac{1}{2}$x+1=1，
∴點圖象G向下平移1個單位時，點A在直線BC上，
當x=4時，y=$\frac{1}{2}$x+1=3，
∴點圖象G向下平移3個單位時，點D在直線BC上，
∴當1＜t≤3時，圖象G向下平移t（t＞0）個單位后與直線BC只有一個公共點．

點評 本題考查了二次函數(shù)圖象與幾何變換：由于拋物線平移后的形狀不變，故a不變，所以求平移后的拋物線解析式通常可利用兩種方法：一是求出原拋物線上任意兩點平移后的坐標，利用待定系數(shù)法求出解析式；二是只考慮平移后的頂點坐標，即可求出解析式．也考查了待定系數(shù)法求函數(shù)解析式．