
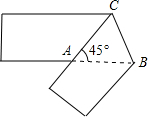
 如圖,將寬為1cm的長方形紙條沿BC折疊,使∠CAB=45°,則折疊后重疊部分的面積為( )
如圖,將寬為1cm的長方形紙條沿BC折疊,使∠CAB=45°,則折疊后重疊部分的面積為( )| A. | $\frac{\sqrt{3}}{2}$ cm2 | B. | $\sqrt{3}$ cm2 | C. | $\sqrt{2}$ cm2 | D. | $\frac{\sqrt{2}}{2}$ cm2 |
分析 如圖,作CH⊥AB于H.首先證明AC-=AB,△ACH是等腰直角三角形,求出AB、CH即可解決問題.
解答 解:如圖,作CH⊥AB于H.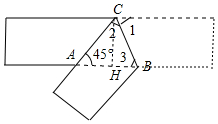
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AC=AB,
∵∠CAB=45°,∠AHC=90°,
∴∠CAH=∠HCA=45°,
∴AH=CH=1,AC=AB=$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$•AB•CH=$\frac{\sqrt{2}}{2}$,
故選D.
點評 本題考查翻折變換、矩形性質、三角形的面積公式等知識,熟知圖形翻折不變性的性質是解答此題的關鍵,本題的突破點是證明AC=AB=$\sqrt{2}$,屬于中考常考題型.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:選擇題
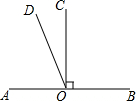 如圖,已知直線AB,線段CO⊥AB于點O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度數為( )
如圖,已知直線AB,線段CO⊥AB于點O,∠AOD=$\frac{1}{2}$∠BOD,∠COD的度數為( )| A. | 15° | B. | 25° | C. | 30° | D. | 45° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com