
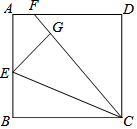
 如圖,已知正方形ABCD,E是AB的中點,F是AD上的一點,EG⊥CF于G且AF=$\frac{1}{4}$AD.
如圖,已知正方形ABCD,E是AB的中點,F是AD上的一點,EG⊥CF于G且AF=$\frac{1}{4}$AD.分析 (1)由正方形的性質得出AB=BC=CD=AD,∠A=∠B=∠C=∠D=90°,證出$\frac{AE}{BC}=\frac{AF}{BE}$=$\frac{1}{2}$,得出△AEF∽△BCE,由相似三角形的性質得出∠AEF=∠BCE,$\frac{EF}{CE}$=$\frac{1}{2}$=$\frac{BE}{BC}$,證出△ECF∽△BCE,得出∠FCE=∠BCE即可;
(2)由射影定理得:EG2=CG•FG,由AAS證明△BCE≌△GCE(AAS),得出BE=EG=$\frac{1}{2}$AB,即可得出結論.
解答 (1)證明:連接EF,如圖所示:
∵正方形ABCD,E是AB的中點,
∴∠A=∠B=90°,AB=BC=AD=CD=2AE=2BE,
∵AF=$\frac{1}{4}$AD,
∴AE=BE=2AF,
∴$\frac{AE}{BC}=\frac{AF}{BE}$=$\frac{1}{2}$,
∴△AEF∽△BCE,
∴∠AEF=∠BCE,$\frac{EF}{CE}$=$\frac{1}{2}$=$\frac{BE}{BC}$,
∵∠BEC+∠BCE=90°,
∴∠BEC+∠AEF=90°,
∴∠FEC=90°=∠B,
∴△ECF∽△BCE,
∴∠FCE=∠BCE,
∴CE平分∠BCF.
(2)證明:∵EG⊥CF,
∴由射影定理得:EG2=CG•FG,
在△BCE和△GCE中,$\left\{\begin{array}{l}{∠B=∠CGE=90°}&{\;}\\{∠BCE=∠GCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△BCE≌△GCE(AAS),
∴BE=EG=$\frac{1}{2}$AB,
∴$\frac{1}{4}$AB2=CG•FG.
點評 本題考查了正方形的性質、相似三角形的判定與性質、全等三角形的判定與性質等知識;本題綜合性強,有一定難度,證明三角形相似和三角形全等是解決問題的關鍵.


科目:初中數學 來源:2016-2017學年湖北省枝江市八年級3月調研考試數學試卷(解析版) 題型:判斷題
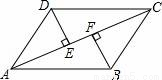
已知:如圖,□ABCD中,DE⊥AC于E,BF⊥AC于F.求證:DE=BF.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
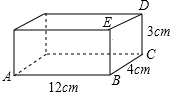 如圖是一個長、寬、高分別為12cm,4cm,3cm的木箱,在它里面放入一根細木條(木條的粗細忽略不計),要求木條不能露出木箱,請你算一算,能放入的細木條的最大長度是多少?
如圖是一個長、寬、高分別為12cm,4cm,3cm的木箱,在它里面放入一根細木條(木條的粗細忽略不計),要求木條不能露出木箱,請你算一算,能放入的細木條的最大長度是多少?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 月用電量(度) | 50度有以下部分 | 超過50度但不超過200度部分 | 超過200度以上部分 |
| 單價(元/度) | 0.53 | 0.56 | 0.63 |
| 月用電量(度) | 230度有以下部分 | 超過230度但不超過400度部分 | 超過400度以上部分 |
| 單價(元/度) | 0.53 | 0.58 | 0.83 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
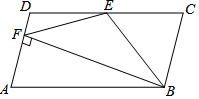 如圖,在平行四邊形ABCD中,AB=2AD,BE平分∠ABC交CD于點E,作BF⊥AD,垂足F在線段AD上,連接EF.則下列結論一定成立的是( )
如圖,在平行四邊形ABCD中,AB=2AD,BE平分∠ABC交CD于點E,作BF⊥AD,垂足F在線段AD上,連接EF.則下列結論一定成立的是( )| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com