
 如圖,以∠AOB的頂點為圓心,取適當長為半徑畫弧,交OA于點C,交OB于點D,再分別以點C、D為圓心,大于$\frac{1}{2}$CD的長為半徑畫弧,兩弧在∠AOB內部交于點E,過點E作射線OE,連接CD.則下列說法錯誤的是( )
如圖,以∠AOB的頂點為圓心,取適當長為半徑畫弧,交OA于點C,交OB于點D,再分別以點C、D為圓心,大于$\frac{1}{2}$CD的長為半徑畫弧,兩弧在∠AOB內部交于點E,過點E作射線OE,連接CD.則下列說法錯誤的是( )| A. | 射線OE是∠AOB的平分線 | B. | O、E兩點關于CD所在直線對稱 | ||
| C. | △COD是等腰三角形 | D. | C、D兩點關于OE所在直線對稱 |
分析 連接CE、DE,根據作圖得到OC=OD、CE=DE,利用SSS證得△EOC≌△EOD從而證明得到射線OE平分∠AOB,判斷A正確;
根據作圖不能得出CD平分OE,判斷B錯誤;
根據作圖得到OC=OD,判斷C正確;
根據作圖得到OC=OD,由A得到射線OE平分∠AOB,根據等腰三角形三線合一的性質得到OE是CD的垂直平分線,判斷D正確.
解答 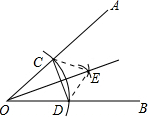 解:A、連接CE、DE,根據作圖得到OC=OD、CE=DE.
解:A、連接CE、DE,根據作圖得到OC=OD、CE=DE.
∵在△EOC與△EOD中,
$\left\{\begin{array}{l}{OC=OD}\\{CE=DE}\\{OE=OE}\end{array}\right.$,
∴△EOC≌△EOD(SSS),
∴∠AOE=∠BOE,即射線OE是∠AOB的平分線,正確,不符合題意;
B、根據作圖不能得出CD平分OE,
∴CD不是OE的平分線,
∴O、E兩點關于CD所在直線不對稱,錯誤,符合題意.
C、根據作圖得到OC=OD,
∴△COD是等腰三角形,正確,不符合題意;
D、根據作圖得到OC=OD,
又∵射線OE平分∠AOB,
∴OE是CD的垂直平分線,
∴C、D兩點關于OE所在直線對稱,正確,不符合題意.
故選B.
點評 本題考查了作圖-基本作圖,全等三角形的判定與性質,角平分線的性質,等腰三角形、軸對稱的性質,從作圖語句中提取正確信息是解題的關鍵.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:初中數學 來源: 題型:填空題
 如圖所示,⊙O的面積為1,點P為⊙O上一點,令記號【n,m】表示半徑OP從如圖所示的位置開始以點O為中心連續旋轉n次后,半徑OP掃過的面積.旋轉的規則為:第1次旋轉m度;第2次從第1次停止的位置向相同的方向再次旋轉$\frac{m}{2}$度:第3次從第2次停止的位置向相同的方向再次旋轉$\frac{m}{4}$度;第4次從第3次停止的位置向相同的方向再次旋轉$\frac{m}{8}$度…依此類推.例如【2,90】=$\frac{3}{8}$,則【2017,180】=$\frac{{2}^{2017}-1}{{2}^{2017}}$.
如圖所示,⊙O的面積為1,點P為⊙O上一點,令記號【n,m】表示半徑OP從如圖所示的位置開始以點O為中心連續旋轉n次后,半徑OP掃過的面積.旋轉的規則為:第1次旋轉m度;第2次從第1次停止的位置向相同的方向再次旋轉$\frac{m}{2}$度:第3次從第2次停止的位置向相同的方向再次旋轉$\frac{m}{4}$度;第4次從第3次停止的位置向相同的方向再次旋轉$\frac{m}{8}$度…依此類推.例如【2,90】=$\frac{3}{8}$,則【2017,180】=$\frac{{2}^{2017}-1}{{2}^{2017}}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
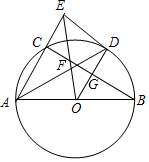 如圖,AB為⊙O的直徑,AC為弦,∠BAC的平分線交⊙O于D,過D作⊙O的切線交AC的延長線于E,OE交AD于F.
如圖,AB為⊙O的直徑,AC為弦,∠BAC的平分線交⊙O于D,過D作⊙O的切線交AC的延長線于E,OE交AD于F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,已知正方形ABCD,頂點A(1,3)、B(1,1)、C(3,1)規定“把正方形ABCD先沿x軸翻折,再向左平移1個單位”為一次變換,如此這樣,連續經過2017次變換后,正方形ABCD的對角線交點M的坐標變為( )
如圖,已知正方形ABCD,頂點A(1,3)、B(1,1)、C(3,1)規定“把正方形ABCD先沿x軸翻折,再向左平移1個單位”為一次變換,如此這樣,連續經過2017次變換后,正方形ABCD的對角線交點M的坐標變為( )| A. | (-2016,2) | B. | (-2016,-2) | C. | (-2015,-2) | D. | (-2015,2) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com