
分析 根據拋物線的解析式求出A、B的坐標,再求出點C的坐標及頂點P的坐標,設拋物線的對稱軸與x軸交于點Q,再根據S四邊形ABPC=S△AOP+S四邊形OCPQ+S△PQB,計算即可求解.
解答 解:令x=0,得:y=2-8=-6,即點C(0,-6),
令y=0得:2(x-1)2-8=0,
解得:x=-1或x=3,
即點A(-1,0)、B(3,0),
頂點P的坐標為(1,-8),
如圖,過點P作PQ⊥x軸于點Q,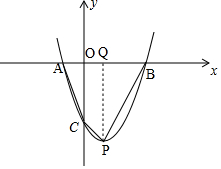
則S四邊形ABPC=S△AOP+S四邊形OCPQ+S△PQB
=$\frac{1}{2}$×1×6+$\frac{1}{2}$×(6+8)×1+$\frac{1}{2}$×8×2
=3+7+8
=18.
點評 本題考查了拋物線與x軸的交點以及二次函數的性質,得出各點的坐標是解答本題的突破口,另外注意將不規則圖形的面積轉化為幾個規則圖形的面積和進行求解.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
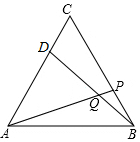 如圖,在等邊△ABC的頂點B、C處各有一只蝸牛,它們同時出發,分別都以每分鐘1個單位的速度由C向A和由B向C爬行,其中一只蝸牛爬到終點時,另一只也停止運動,經過t分鐘后,它們分別爬行到D、P處,請問:
如圖,在等邊△ABC的頂點B、C處各有一只蝸牛,它們同時出發,分別都以每分鐘1個單位的速度由C向A和由B向C爬行,其中一只蝸牛爬到終點時,另一只也停止運動,經過t分鐘后,它們分別爬行到D、P處,請問:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
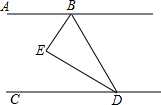 如圖,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直線CD上一動點,(不與點D重合),BI平分∠HBD,寫出∠EBI與∠BHD的數量關系,并說明理由.
如圖,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,H是直線CD上一動點,(不與點D重合),BI平分∠HBD,寫出∠EBI與∠BHD的數量關系,并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
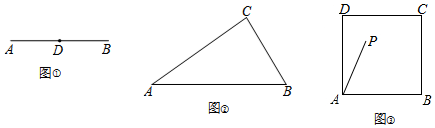
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com