Question

8．已知直線y=$\frac{4}{3}$x-4與x軸和y軸的交點分別為A、B．
（1）求△ABO的面積；
（2）求△ABO的邊AB上的高；
（3）求x軸上的一點C，使∠ABC=90°．

Answer 1

分析 （1）先求得A、B的坐標，從而求得OA=3，OB=4，然后根據(jù)三角形面積公式求得即可；
（2）作OD⊥AB于D，根據(jù)勾股定理求得AB=5，然后根據(jù)三角形面積公式得到$\frac{1}{2}$AB•OD=6，從而求得OD的值；
（3）根據(jù)蛇油=射影定理得到OB²=OC•OA，從而求得OC的長，即可求得C的坐標．

解答 解：（1）∵直線y=$\frac{4}{3}$x-4與x軸和y軸的交點分別為A、B．
∴令y=0，求得x=3，令x=0，求得y=-4，
∴A（3，0），B（0，-4），
∴△ABO的面積：$\frac{1}{2}$×3×4=6；
（2）∵OA=3，OB=4，
∴根據(jù)勾股定理求得AB=5，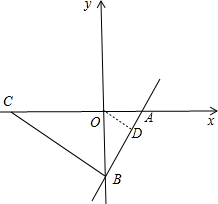
如圖，作OD⊥AB于D，
∵$\frac{1}{2}$AB•OD=6，
∴OD=$\frac{12}{5}$，
∴△ABO的邊AB上的高為$\frac{12}{5}$；
（3）如圖，∵∠ABC=90°，
∴OB²=OC•OA，
∴OC=$\frac{O{B}^{2}}{OA}$=$\frac{{4}^{2}}{3}$=$\frac{16}{3}$，
∴C（-$\frac{16}{3}$，0）．

點評 此題考查了一次函數(shù)圖象上點的坐標特征以及三角形面積的綜合運用，本題要求學(xué)生掌握一次函數(shù)與坐標軸交點的求法，與x軸交點的橫坐標為令y=0求出的x的值；與y軸交點的縱坐標為令x=0求出的y的值，確定出與坐標軸的交點坐標．一次函數(shù)的圖象與兩坐標軸常圍成直角三角形，解決這類問題一般需要利用點的坐標表示出線段的長度，從而根據(jù)三角形的面積公式來求解．