Question

11．如圖，在矩形AOBC中，點A的坐標是（-2，1），點C的縱坐標是4，則B、C兩點的坐標分別是（　　）

• A． （$\frac{2}{3}$，3），（-$\frac{1}{2}$，4）
• B． （$\frac{7}{4}$，$\frac{7}{2}$），（$-\frac{1}{2}$，4）
• C． （$\frac{2}{3}$，3），（$-\frac{2}{3}$，4）
• D． （$\frac{7}{4}$，$\frac{7}{2}$），（$-\frac{2}{3}$，4）

Answer 1

分析 先過點A作AD⊥x軸于點D，過點B作BE⊥x軸于點E，過點C作CF∥y軸，過點A作AF∥x軸，交點為F，易得△CAF≌△BOE，△AOD∽△OBE，然后由相似三角形的對應邊成比例求得答案．

解答 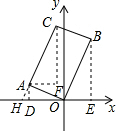解：如圖，過點A作AD⊥x軸于點D，過點B作BE⊥x軸于點E，過點C作CF∥y軸，過點A作AF∥x軸，交點為F，延長CA交x軸于點H，
∵四邊形AOBC是矩形，
∴AC∥OB，AC=OB，
∴∠CAF=∠BOE=∠CHO，
在△ACF和△OBE中，
$\left\{\begin{array}{l}{∠F=∠BEO=90°}\\{∠CAF=∠BOE}\\{AC=OB}\end{array}\right.$，
∴△CAF≌△BOE（AAS），
∴BE=CF=4-1=3，
∵∠AOD+∠BOE=∠BOE+∠OBE=90°，
∴∠AOD=∠OBE，
∵∠ADO=∠OEB=90°，
∴△AOD∽△OBE，
∴$\frac{AD}{OE}$=$\frac{OD}{BE}$，
即$\frac{1}{OE}$=$\frac{2}{3}$，
∴OE=$\frac{3}{2}$，即點B（$\frac{3}{2}$，3），
∴AF=OE=$\frac{3}{2}$，
∴點C的橫坐標為：-（2-$\frac{3}{2}$）=-$\frac{1}{2}$，
∴點C（-$\frac{1}{2}$，4）．
故選：A．

點評 此題考查了矩形的性質、全等三角形的判定與性質以及相似三角形的判定與性質．此題注意掌握輔助線的作法，注意掌握數形結合思想的應用．