
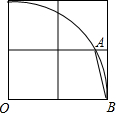
 如圖,在2×2的網格中,以頂點O為圓心,以2個單位長度為半徑作圓弧,交圖中格線于點A,則tan∠ABO的值為2+$\sqrt{3}$.
如圖,在2×2的網格中,以頂點O為圓心,以2個單位長度為半徑作圓弧,交圖中格線于點A,則tan∠ABO的值為2+$\sqrt{3}$. 分析 連接OA,過點A作AC⊥OB于點C,由題意知AC=1、OA=OB=2,從而得出OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{3}$、BC=OB-OC=2-$\sqrt{3}$,在Rt△ABC中,根據tan∠ABO=$\frac{AC}{BC}$可得答案.
解答 解:如圖,連接OA,過點A作AC⊥OB于點C,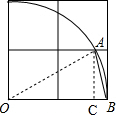
則AC=1,OA=OB=2,
∵在Rt△AOC中,OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴BC=OB-OC=2-$\sqrt{3}$,
∴在Rt△ABC中,tan∠ABO=$\frac{AC}{BC}$=$\frac{1}{2-\sqrt{3}}$=2+$\sqrt{3}$.
故答案是:2+$\sqrt{3}$.
點評 本題主要考查解直角三角形,根據題意構建一個以∠ABO為內角的直角三角形是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
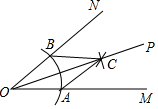 如圖,用尺規作∠MON的平分線OP.由作圖知△OAC≌△OBC,從而得OP平分∠MON,則此兩個三角形全等的依據是( )
如圖,用尺規作∠MON的平分線OP.由作圖知△OAC≌△OBC,從而得OP平分∠MON,則此兩個三角形全等的依據是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
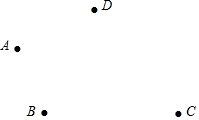 如圖,平面上有四個點A,B,C,D,按照以下要求完成問題:
如圖,平面上有四個點A,B,C,D,按照以下要求完成問題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 測量該四邊形的對角線是否互相垂直 | |
| B. | 測量該四邊形的對角線是否相等 | |
| C. | 測量該四邊形的對角線是否互相平分 | |
| D. | 測量該四邊形的四條邊是否都相等 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-3,7) | B. | (-7,3) | C. | (3,7) | D. | (7,3) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com