
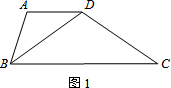
 我們把有一組鄰邊相等,一組對邊平行但不相等的四邊形稱作“準菱形”.
我們把有一組鄰邊相等,一組對邊平行但不相等的四邊形稱作“準菱形”.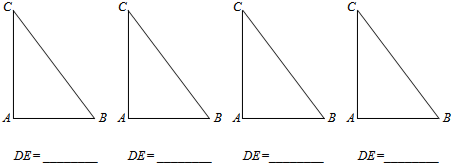
分析 (1)根據準菱形的定義寫出已知,結合圖形寫出求證,利用平行線的性質定理進行證明;
(2)分AE=AB,DE∥AB、BA=BD,DE∥AB、EA=ED,DE∥AB、DE=BD,DE∥AB四種情況,利用相似三角形的判定定理和性質定理計算即可.
解答 解:(1)已知:如圖,“準菱形”ABCD中,AB=AD,AD∥BC,(AD≠BC).
求證:BD平分∠ABC.
證明: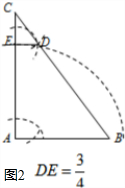
∵AB=AD,
∴∠ABD=∠BDA,
又∵AD∥BC,
∴∠DBC=∠BDA.
∴∠ABD=∠DBC.
即BD平分∠ABC;
故答案為:如圖,“準菱形”ABCD中,AB=AD,AD∥BC,(AD≠BC);BD平分∠ABC;∵AB=AD,∴∠ABD=∠BDA,又∵AD∥BC,∴∠DBC=∠BDA.∴∠ABD=∠DBC.即BD平分∠ABC;
(2)可以作出如下四種圖形,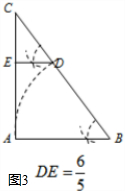
∵∠A=90°,AB=3,AC=4,
∴BC=5,
如圖2,當AE=AB,DE∥AB時,
$\frac{DE}{AB}$=$\frac{CE}{CA}$,即$\frac{DE}{3}$=$\frac{1}{4}$,
解得,DE=$\frac{3}{4}$;
如圖3,當BA=BD,DE∥AB時,
$\frac{DE}{AB}$=$\frac{CD}{CB}$,即$\frac{DE}{3}$=$\frac{2}{5}$,
解得,DE=$\frac{6}{5}$;
如圖4,當EA=ED,DE∥AB時,
$\frac{DE}{AB}$=$\frac{CE}{CA}$,即$\frac{DE}{3}$=$\frac{4-DE}{4}$,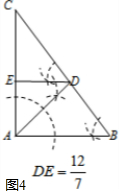
解得,DE=$\frac{12}{7}$;
如圖5,當DE=BD,DE∥AB時,
$\frac{DE}{AB}$=$\frac{CD}{CB}$,即$\frac{DE}{3}$=$\frac{5-DE}{5}$,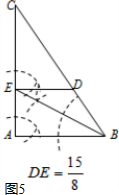
解得,DE=$\frac{15}{8}$.
點評 本題考查的是新定義、相似三角形的判定和性質,正確理解準菱形的定義、靈活運用相似三角形的判定定理和性質定理是解題的關鍵,在解答時注意分情況討論思想是靈活運用.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某藝術類學校進行繪畫特長生的招生工作,每名考生需要參加“素描”“色彩”“速寫”三個項目的測試,三個項目的滿分均為100分,“素描”“色彩”“速寫”按照4:4:2的比例計算得到選手最終成就,現有20名考生報名參加測試,測試結束后,考生的素描成績如下(單位:分):
某藝術類學校進行繪畫特長生的招生工作,每名考生需要參加“素描”“色彩”“速寫”三個項目的測試,三個項目的滿分均為100分,“素描”“色彩”“速寫”按照4:4:2的比例計算得到選手最終成就,現有20名考生報名參加測試,測試結束后,考生的素描成績如下(單位:分):| 分組 | 人數(頻數) |
| 60-70 | 1 |
| 70-80 | 2 |
| 80-90 | 9 |
| 90-100 | 8 |
| 合計 | 20 |
| 項目 成績 | 素描 | 色彩 | 速寫 |
| 甲 | 98 | 93 | 95 |
| 乙 | 95 | 95 | 100 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
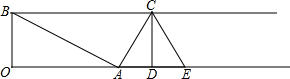 如圖,射線BC∥射線OA,BO⊥OA,且OB=2,OA=4,過點A作AC⊥AB交射線BC于C,過點C作CD⊥射線OA交射線OA于D,A,E關于直線CD對稱,將△CDE沿射線BC向左向右平移得到△C′D′E′.再將以A,B,C′,E′為頂點的四邊形沿著C′D′剪開得到的兩個圖形拼成不重疊無縫隙的圖形恰好是三角形,請寫出所有符合上述條件的BC′的長6或1.
如圖,射線BC∥射線OA,BO⊥OA,且OB=2,OA=4,過點A作AC⊥AB交射線BC于C,過點C作CD⊥射線OA交射線OA于D,A,E關于直線CD對稱,將△CDE沿射線BC向左向右平移得到△C′D′E′.再將以A,B,C′,E′為頂點的四邊形沿著C′D′剪開得到的兩個圖形拼成不重疊無縫隙的圖形恰好是三角形,請寫出所有符合上述條件的BC′的長6或1.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.25≤x<1.35 | B. | 1.295≤x<1.305 | C. | 1.25<x<1.35 | D. | 1.295<x<1.305 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com