Question

10．如圖，直角坐標系中A（1，0），B（0，2），∠BCA=90°，BC=AC，求C點的坐標．

Answer 1

分析 過C作CD⊥y軸，CE⊥x軸，利用AAS證明△CBD與△CAE全等，再利用勾股定理進行解答求得BC=AC=$\frac{\sqrt{10}}{2}$，根據S_{正方形DOEC}=S_{四邊形ACBO}=S_△AOB+S_△ACB=$\frac{1}{2}×1×2+\frac{1}{2}×\frac{\sqrt{10}}{2}×\frac{\sqrt{10}}{2}$=$\frac{9}{4}$，求得CD=CE=$\frac{3}{2}$，即可得到結論．

解答 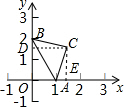解：過C作CD⊥y軸于D，CE⊥x軸于E，
則∠BDC=∠AEC=90°，
∵∠BCA=90°，
∴∠BCD=∠ACE=90°-∠DCA，
在△BDC和△AEC中，
$\left\{\begin{array}{l}{∠BCD=∠ACE}\\{∠BDC=∠AEC}\\{BC=AC}\end{array}\right.$，
∴△BDC≌△AEC，
∴DC=CE，
∴四邊形DOEC是正方形，
∵BC²+AC²=AB²=OB²+OA²=2²+1²=5，
∴BC=AC=$\frac{\sqrt{10}}{2}$，
∴S_{正方形DOEC}=S_{四邊形ACBO}=S_△AOB+S_△ACB=$\frac{1}{2}×1×2+\frac{1}{2}×\frac{\sqrt{10}}{2}×\frac{\sqrt{10}}{2}$=$\frac{9}{4}$，
∴CD=CE=$\frac{3}{2}$，
∴C點的坐標（$\frac{3}{2}$，$\frac{3}{2}$）．

點評 本題考查了全等三角形的判定，考查了全等三角形對應邊相等的性質，坐標與圖形的性質，本題中求證△ACE≌△CDB是解題的關鍵．