
如圖, 在平面直角坐標系中,點A,B分別是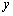 軸正半軸,
軸正半軸,  軸正半軸上兩動點,
軸正半軸上兩動點,  ,
, ,以AO,BO為鄰邊構造矩形AOBC,拋物線
,以AO,BO為鄰邊構造矩形AOBC,拋物線 交
交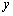 軸于點D,P為頂點,PM⊥
軸于點D,P為頂點,PM⊥ 軸于點M.
軸于點M.
(1)求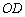 ,
, 的長(結果均用含
的長(結果均用含 的代數式表示).
的代數式表示).
(2)當 時,求該拋物線的表達式.
時,求該拋物線的表達式.
(3)在點 在整個運動過程中.
在整個運動過程中.
①若存在 是等腰三角形,請求出所有滿足條件的
是等腰三角形,請求出所有滿足條件的 的值.
的值.
 ②當點A關于直線DP的對稱點
②當點A關于直線DP的對稱點 恰好落在拋物線
恰好落在拋物線 的圖象上時,請直接寫出
的圖象上時,請直接寫出 的值.
的值.
解:(1)把x=0,代入 ,得
,得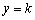 .∴
.∴ .
.
∵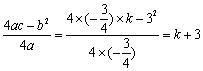 ,∴
,∴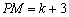 . (3分)
. (3分)
(2)∵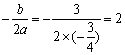 ,∴
,∴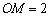 ,
,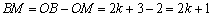 .
.
又∵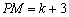 ,
, ,∴
,∴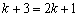 ,解得
,解得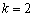 .
.
∴該拋物線的表達式為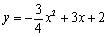 . (3分)
. (3分)
(3)①
Ⅰ)當點P在矩形AOBC外部時
如圖1,過P作PK⊥OA于點K,當AD=AP時,
∵AD=AO-DO=2k-k=k,
∴AD=AP =k,KA=KO-AO=PM-AO=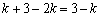
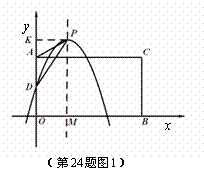 KP=OM=2,在Rt△KAP中,
KP=OM=2,在Rt△KAP中,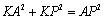
∴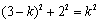 ,解得
,解得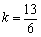 .
.
Ⅱ)當點P在矩形AOBC內部時
當PD=AP時,如圖2,過P作PH⊥OA于H,
AD=k,HD=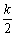 ,
,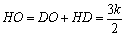
又∵HO=PM=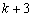 ,
,
∴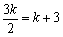 ,解得
,解得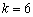 .
.
當DP=DA時,如圖3,過D作PQ⊥PM于Q,
PQ=PM-QM=PM-OD=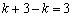
DQ=OM=2,DP=DA=k,
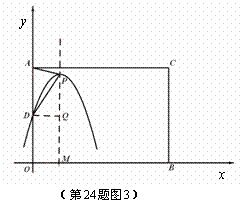
在Rt△DQP中,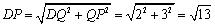 .
.
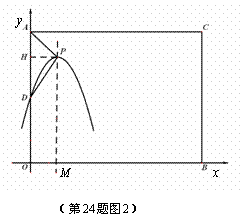
∴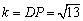 . (6分)
. (6分)
② .
.
 | |||
 | |||


 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
如圖,在邊長為4的正方形ABCD中,點P在AB上從A向B運動,連接DP交AC于點Q.
(1)試證明:無論點P運動到AB上何處時,都有△ADQ≌△ABQ;
(2)當點P在AB上運動到什么位置時,△ADQ的面積是正方形ABCD面積的
 ;
;
(3)若點P從點A運動到點B,再繼續在BC上運動到點C,在整個運動過程中,當點P運動到什么位置時,△ADQ恰為等腰三角形.


查看答案和解析>>
科目:初中數學 來源: 題型:
在一個不透明的口袋里裝有1個紅球,2個白球和n個黃球,這些球除顏色外其余都相同.若從該口袋中任意摸出1個球,摸到白球的可能性大于黃球的可能性,則n等于 .
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,在平面直角坐標系中,已知點A(3,4),B( 3,0).
3,0).
(1)只用直尺(沒有刻度)和圓規按下列要求作圖.
(要求:保留作圖痕跡,不必寫出作法)
Ⅰ)AC⊥y軸,垂足為C;
Ⅱ)連結AO,AB,設邊AB,CO交點E.
(2)在(1)作出圖形后,直接判斷△AOE與△BOE的面積大小關系.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com