Question

10．如圖，半徑為2的⊙O與正五邊形ABCDE的兩邊AE、CD相切于點A、C，則劣弧$\widehat{AC}$長度為（　　）

• A． $\frac{3}{5}$π
• B． $\frac{4}{5}$π
• C． $\frac{8}{5}$π
• D． $\frac{2}{3}$π

Answer 1

分析 連接OA、OC，根據切線的性質得到∠OAE=90°，∠OCD=90°，根據正多邊形的內角和公式求出正五邊形的內角的度數，求出∠AOC的度數，利用弧長公式計算即可．

解答 解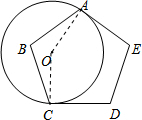：連接OA、OC，
∵AE、CD切⊙O于點A、C，
∴∠OAE=90°，∠OCD=90°，
正五邊形ABCDE的每個內角的度數為$\frac{（5-2）×180°}{5}$=108°，
∴∠AOC=540°-90°-90°-108°-108°=144°，
∴$\widehat{AC}$長度=$\frac{144π×2}{180}$=$\frac{8}{5}π$，
故選：C．

點評 本題考查的是弧長的計算和正多邊形的內角和公式的應用，掌握弧長的計算公式：l=$\frac{nπr}{180}$是解題的關鍵．