
 如圖,圓E是三角形ABC的外接圓,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分別以BC、AO所在直線建立x軸.
如圖,圓E是三角形ABC的外接圓,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分別以BC、AO所在直線建立x軸.分析 (1)如圖1中,連接EB、EC.由BC=OB+OC=5,∠BEC=2∠BC=90°,可知EB=EC=$\frac{5\sqrt{2}}{2}$.
(2)如圖2中,作EM⊥BC于M,EN⊥OA于N,連接AE,則四邊形EMON是矩形.利用勾股定理求出點A、B、C三點坐標,利用待定系數法即可解決問題.
(3)①以OA為直徑畫圓與拋物線有4個交點,根據直徑所對的圓周角是直角,可知這樣有4個點P滿足條件.②當PA⊥OA時,有一個點P滿足條件.③當PO⊥OA時,有兩個點P滿足條件.
解答 解:(1)如圖1中,連接EB、EC.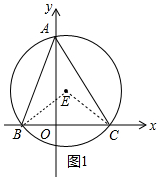
∵BC=OB+OC=5,∠BEC=2∠BC=90°,
∴EB=EC=$\frac{5\sqrt{2}}{2}$,
∴⊙E的直徑為$5\sqrt{2}$.
(2)如圖2中,作EM⊥BC于M,EN⊥OA于N,連接AE,則四邊形EMON是矩形.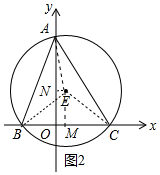
在Rt△EMC中,EM=ON=$\sqrt{E{C}^{2}-C{M}^{2}}$=$\sqrt{(\frac{5\sqrt{2}}{2})^{2}+(\frac{5}{2})^{2}}$=$\frac{5}{2}$,OM=NE=OC-CM=$\frac{1}{2}$,
在Rt△EN中,AN=$\sqrt{A{E}^{2}-E{N}^{2}}$=$\sqrt{(\frac{5\sqrt{2}}{2})^{2}-(\frac{1}{2})^{2}}$=$\frac{7}{2}$,
∴OA=AN+ON=6,
∴A(0,6),B(-2,0),C(3,0),
設拋物線的解析式為y=a(x+2)(x-3),把(0,6)的坐標代入得a=-1,
∴拋物線的解析式為y=-x2+x+6.
(3)如圖3中,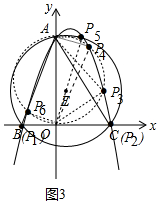
①以OA為直徑畫圓與拋物線有4個交點,根據直徑所對的圓周角是直角,可知這樣有4個點P滿足條件.
②當PA⊥OA時,有一個點P滿足條件.
③當PO⊥OA時,有兩個點P滿足條件.
所以滿足條件的點P有6個.
點評 本題考查二次函數綜合題、圓的有關知識、勾股定理、待定系數法等知識,解題的關鍵是學會添加常用輔助線,構造直角三角形解決問題,學會利用直徑所對的圓周角是直角尋找直角,所以中考壓軸題.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:初中數學 來源: 題型:選擇題
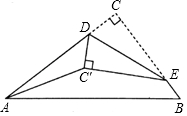 如圖,在△ABC中,∠C=90°,AC=4cm,BC=3cm,點D、E分別在AC、BC上.現將△DCE沿DE翻折,使點C落在點C'處.連接AC',則AC'長度的最小值.( )
如圖,在△ABC中,∠C=90°,AC=4cm,BC=3cm,點D、E分別在AC、BC上.現將△DCE沿DE翻折,使點C落在點C'處.連接AC',則AC'長度的最小值.( )| A. | 不存在 | B. | 等于1cm | C. | 等于2 cm | D. | 等于2.5 cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com