
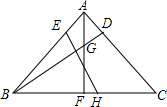
 如圖,△ABC,AB=AC,∠BAC=90°,點(diǎn)D,E分別在AC,AB上,AD=AE,△ABC的高AF交BD于G,過(guò)點(diǎn)E作BD的垂線(xiàn)交BC于點(diǎn)H,若GF=3,CH=4,則點(diǎn)A到BD的距離為$\frac{5}{17}$$\sqrt{34}$.
如圖,△ABC,AB=AC,∠BAC=90°,點(diǎn)D,E分別在AC,AB上,AD=AE,△ABC的高AF交BD于G,過(guò)點(diǎn)E作BD的垂線(xiàn)交BC于點(diǎn)H,若GF=3,CH=4,則點(diǎn)A到BD的距離為$\frac{5}{17}$$\sqrt{34}$. 分析 如圖,作AM⊥EH于M,AN⊥BD于N交BC于T,CK⊥AT于K交EH的延長(zhǎng)線(xiàn)于P,BD交EH于Q.連接AQ.首先證明AQ平分∠EQD,推出四邊形AMQN是正方形,由△ABN≌△CAK,推出AM=CK,PK=CK,由TK∥PH,推出CT=TH=2,由△BFN≌△AFT,推出NF=TF=3,F(xiàn)H=1,BF=CF=5,在Rt△BNF中,可得BN=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$,
由△CTK∽△BNF,得到$\frac{CK}{BF}$=$\frac{CT}{BN}$,求出CK即可解決問(wèn)題.
解答 解:如圖,作AM⊥EH于M,AN⊥BD于N交BC于T,CK⊥AT于K交EH的延長(zhǎng)線(xiàn)于P,BD交EH于Q.連接AQ.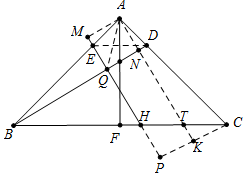
∵AE=AD,∠EAD=90°,
∴∠ADE=∠AED=45°,
∵EH⊥BD,
∴∠EQD=90°,
∴∠EQD+∠EAD=180°,
∴A、E、Q、D四點(diǎn)共圓,
∴∠AQE=∠ADE=45°,∠AQD=∠AED=45°,
∴AQ平分∠EQD,∵AM⊥MQ,AN⊥QD,
∴AM=AN,則易知四邊形AMQN是正方形,四邊形AMPK是矩形,
∴AM=PK,
在△ABN和△CAK中,
$\left\{\begin{array}{l}{∠ABN=∠CAK}\\{∠ANB=∠AKC}\\{AB=AC}\end{array}\right.$,
∴△ABN≌△CAK,
∴AM=CK,
∴PK=CK,
∵TK∥PH,
∴CT=TH=2,
在△BFN和△AFT中,
$\left\{\begin{array}{l}{∠FBN=∠FAT}\\{BF=AF}\\{∠BFN=∠AFT}\end{array}\right.$,
∴△BFN≌△AFT,
∴NF=TF=3,
∴FH=1,
∴BF=CF=5,
在Rt△BNF中,BF=5,F(xiàn)N=3,
∴BN=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$,
由△CTK∽△BNF,
∴$\frac{CK}{BF}$=$\frac{CT}{BN}$,
∴$\frac{CK}{5}$=$\frac{2}{\sqrt{34}}$,
∴CK=$\frac{5}{17}$$\sqrt{34}$.
∴AN=CK=$\frac{5}{17}$$\sqrt{34}$.
故答案為$\frac{5}{17}$$\sqrt{34}$.
點(diǎn)評(píng) 本題考查全等三角形的判定和性質(zhì)、相似三角形的判定和性質(zhì)、等腰直角三角形的性質(zhì)、四點(diǎn)共圓、角平分線(xiàn)的判定定理、勾股定理等知識(shí),解題的關(guān)鍵是學(xué)會(huì)條件輔助線(xiàn),本題的突破點(diǎn)是證明四邊形AMQN是正方形,屬于中考填空題中的壓軸題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 0.22 | B. | 0.42 | C. | 0.50 | D. | 0.58 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
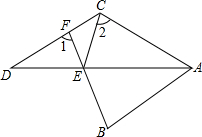 如圖,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延長(zhǎng)線(xiàn)交CD于F,連CE,且∠1=∠2,求證:AB=AC.
如圖,AD平分∠BAC,∠BAC+∠ACD=180°,E在AD上,BE的延長(zhǎng)線(xiàn)交CD于F,連CE,且∠1=∠2,求證:AB=AC.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,在?ABCD中,E是AD邊上的中點(diǎn),連接BE,并延長(zhǎng)BE交CD的延長(zhǎng)線(xiàn)于點(diǎn)F,若△EDF的周長(zhǎng)為9,則△BCF的周長(zhǎng)為18.
如圖,在?ABCD中,E是AD邊上的中點(diǎn),連接BE,并延長(zhǎng)BE交CD的延長(zhǎng)線(xiàn)于點(diǎn)F,若△EDF的周長(zhǎng)為9,則△BCF的周長(zhǎng)為18.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com