
【題目】如圖1,△ABC中,AC=BC,∠ACB=90°,點P為AB上一點(異于A、B),BD⊥直線CP于D,AE⊥直線CP于E,點F為AB的中點,連接DF.
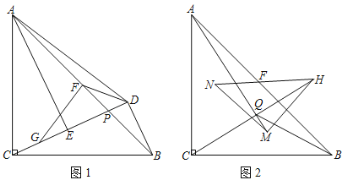
(1)可以把△ACE繞點F逆時針旋轉 度(度數不超過180°)和△ 重合,則∠FDE= °.
(2)取CE的中點G,連接AD、FG,求證:AD=2FG.
(3)如圖2,AB=8,等腰直角△MNH的斜邊NH的中點也為點F,直線AM和直線CH交于點Q,連接BQ,當△MNH繞點F旋轉一周時,請直接寫出BQ長的取值范圍.
【答案】(1)90,CBD,45;(2)見解析;(3)2![]() -2
-2![]() ≤BQ≤2
≤BQ≤2![]() +2
+2![]()
【解析】
(1)由等腰直角三角形的性質可得CF=AF=BF,CF⊥BF,由“AAS”可證△ACE≌△CBD,則可以把△ACE繞點F逆時針旋轉90度和△CBD重合,可得CE=DB,EF=DF,可證△CFE≌△BFD,可得∠CFE=∠BFD,可證∠EFD=90°,可求解;
(2)取BD中點H,連接FH,由中點定義和三角形中位線定理可得CG=![]() CE=
CE=![]() BD=BH,AD∥FH,AD=2FH,由“SAS”可證△CFG≌△BFH,可得GF=FH,可得AD=2FG;
BD=BH,AD∥FH,AD=2FH,由“SAS”可證△CFG≌△BFH,可得GF=FH,可得AD=2FG;
(3)如圖2,連接CF,MF,由全等三角形的性質可求∠AQC=90°,可得點Q在以AC為直徑的圓上運動,即可求解.
(1)如圖1,連接CF,EF,
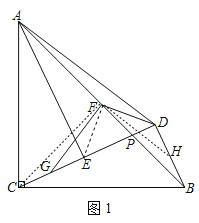
∵AC=BC,∠ACB=90°,點F為AB的中點,
∴CF=AF=BF,CF⊥BF,
∵AE⊥CD,BD⊥CD,
∴∠AEC=∠CDB=∠ACB=90°,
∴∠ACE+∠CAE=90°,∠ACE+∠DCB=90°,
∴∠CAE=∠DCB,且AC=BC,∠AEC=∠CDB=90°,
∴△ACE≌△CBD(AAS)
∴可以把△ACE繞點F逆時針旋轉90度和△CBD重合,
∴CE=DB,EF=DF,且CF=BF,
∴△CFE≌△BFD(SSS)
∴∠CFE=∠BFD,且∠CFE+∠EFB=90°,
∴∠BFD+∠EFB=90°,
∴∠EFD=90°,且EF=DF,
∴∠FDE=45°,
故答案為:90,CBD,45;
(2)如圖1,取BD中點H,連接FH,
∵點G是CE中點,點H是BD中點,點F是AB中點,且CE=BD,
∴CG=![]() CE=
CE=![]() BD=BH,AD∥FH,AD=2FH,
BD=BH,AD∥FH,AD=2FH,
∵△CFE≌△BFD,
∴∠FCG=∠FBH,且CG=BH,CF=BF,
∴△CFG≌△BFH(SAS)
∴GF=FH,
∴AD=2FG;
(3)如圖2,連接CF,MF,
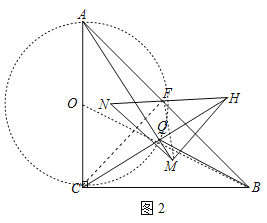
∵AC=BC,∠ACB=90°,點F是AB中點,AB=8,
∴AF=CF=BF=4,CF⊥AB,AC=BC=4![]() ,
,
∵MN=MH,∠NMH=90°,點F是NH中點,
∴NF=FH=FM,MF⊥NH,
∴∠MFH=∠AFC=90°,
∴∠AFM=∠CFH,且AF=CF,FH=FM,
∴△AFM≌△CFH(SAS)
∴∠FAM=∠FCH,
∵∠FAM+∠CAM+∠ACF=90°,
∴∠CAM+∠ACF+∠FCH=90°,
∴∠AQC=90°,
∴點Q在以AC為直徑的圓上運動,
∴當點Q在BO的延長線上時,BQ最大;當點Q在線段BO上時,BQ最小.
取AC中點O,連接BO,
∴CO=2![]() ,
,
∴BO=![]() =
=![]() =2
=2![]() ,
,
∴BQ長的取值范圍為![]()


科目:初中數學 來源: 題型:
【題目】拋物線y1=x2+bx+c與直線y2=2x+m相交于A(1,4)、B(﹣1,n)兩點.
(1)求y1和y2的解析式;
(2)直接寫出y1﹣y2的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:甲袋中裝有黃金9枚(每枚黃金重量相同),乙袋中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲袋比乙袋輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,根據題意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每個小正方形的邊長為1,格點△ABC(頂點在網格線的交點上)的頂點A、C的坐標分別為A(﹣3,5)、C(0,3).
(1)請在網格所在的平面內畫出平面直角坐標系,并寫出點B的坐標.
(2)將△ABC繞著原點順時針旋轉90°得△A1B1C1,畫出△A1B1C1.
(3)在直線y=1上存在一點P,使PA+PC的值最小,請直接寫出點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
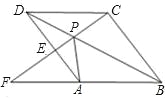
【題目】如圖,點P是菱形ABCD的對角線BD上一點,連接CP并延長,交AD于E,交BA的延長線點F.問:
(1)圖中△APD與哪個三角形全等?并說明理由;
(2)求證:△APE∽△FPA;
(3)猜想:線段PC,PE,PF之間存在什么關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
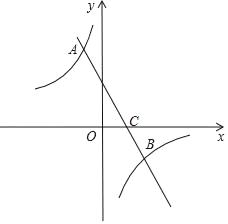
【題目】如圖,直線y=kx+b(k≠0)與雙曲線y=![]() (m≠0)交于點A(﹣
(m≠0)交于點A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直線與雙曲線的解析式.
(2)點P在x軸上,如果S△ABP=3,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系![]() 中的圖形M,N,給出如下定義:如果點P為圖形M上任意一點,點Q為圖形N上任意一點,那么稱線段PQ長度的最小值為圖形M,N的“近距離”,記作 d(M,N).若圖形M,N的“近距離”小于或等于1,則稱圖形M,N互為“可及圖形”.
中的圖形M,N,給出如下定義:如果點P為圖形M上任意一點,點Q為圖形N上任意一點,那么稱線段PQ長度的最小值為圖形M,N的“近距離”,記作 d(M,N).若圖形M,N的“近距離”小于或等于1,則稱圖形M,N互為“可及圖形”.
(1)當⊙O的半徑為2時,
①如果點A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直線![]() 與⊙O互為“可及圖形”,求b的取值范圍;
與⊙O互為“可及圖形”,求b的取值范圍;
(2)⊙G的圓心G在![]() 軸上,半徑為1,直線
軸上,半徑為1,直線![]() 與x軸交于點C,與y軸交于點D,如果⊙G和∠CDO互為“可及圖形”,直接寫出圓心G的橫坐標m的取值范圍.
與x軸交于點C,與y軸交于點D,如果⊙G和∠CDO互為“可及圖形”,直接寫出圓心G的橫坐標m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com