【題目】如圖，在正方形網格中，每個小正方形的邊長為1，格點△ABC（頂點在網格線的交點上）的頂點A、C的坐標分別為A（﹣3，5）、C（0，3）．
（1）請在網格所在的平面內畫出平面直角坐標系，并寫出點B的坐標．
（2）將△ABC繞著原點順時針旋轉90°得△A1B1C1，畫出△A1B1C1．
（3）在直線y＝1上存在一點P，使PA+PC的值最小，請直接寫出點P的坐標．
星級口算天天練系列答案
芒果教輔達標測試卷系列答案科目：初中數學 來源： 題型：
【題目】某工程對承接了60萬平方米的綠化工程，由于情況有變，……，設原計劃每天綠化的面積為
萬平方米，列方程為
，根據方程可知省略的部分是（ ）
A.實際工作時每天的工作效率比原計劃提高了20%，結果提前30天完成了這一任務
B.實際工作時每天的工作效率比原計劃提高了20%，結果延誤30天完成了這一任務
C.實際工作時每天的工作效率比原計劃降低了20%，結果延誤30天完成了這一任務
D.實際工作時每天的工作效率比原計劃降低了20%，結果提前30天完成了這一任務
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，點D為AC中點，點E在BD延長線上，且BD：DE＝3：5，連接CE，tan∠BAC＝
，CB＝
，則線段EC長為_____．
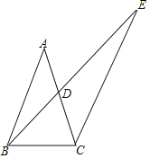
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b（k≠0）的圖象與x軸，y軸分別交于A（﹣9，0），B（0，6）兩點，過點C（2，0）作直線l與BC垂直，點E在直線l位于x軸上方的部分．
（1）求一次函數y=kx+b（k≠0）的表達式；
（2）若△ACE的面積為11，求點E的坐標；
（3）當∠CBE=∠ABO時，點E的坐標為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4cm，點P從點A出發以lcm/s的速度沿折線AC﹣CB運動，過點P作PQ⊥AB于點Q，當點P不與點A、B重合時，以線段PQ為邊向右作正方形PQRS，設正方形PQRS與△ABC的重疊部分面積為S，點P的運動時間為t（s）．
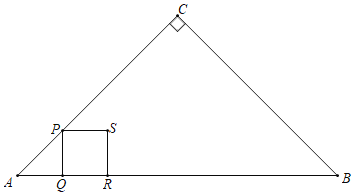
（1）用含t的代數式表示CP的長度；
（2）當點S落在BC邊上時，求t的值；
（3）當正方形PQRS與△ABC的重疊部分不是五邊形時，求S與t之間的函數關系式；
（4）連結CS，當直線CS分△ABC兩部分的面積比為1：2時，直接寫出t的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠BAC=90°，將△ABC繞點A順時針旋轉90°后得到△AB′C′(點B的對應點是點B′，點C的對應點是點C′)，連接CC′，若∠CC′B′=33°，則∠B的大小是( )
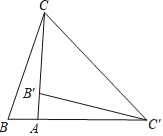
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，△ABC中，AC＝BC，∠ACB＝90°，點P為AB上一點（異于A、B），BD⊥直線CP于D，AE⊥直線CP于E，點F為AB的中點，連接DF．
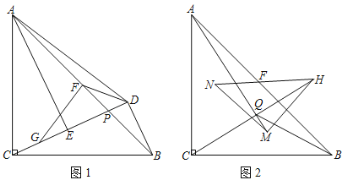
（1）可以把△ACE繞點F逆時針旋轉 度（度數不超過180°）和△ 重合，則∠FDE＝ °．
（2）取CE的中點G，連接AD、FG，求證：AD＝2FG．
（3）如圖2，AB＝8，等腰直角△MNH的斜邊NH的中點也為點F，直線AM和直線CH交于點Q，連接BQ，當△MNH繞點F旋轉一周時，請直接寫出BQ長的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】中華文明，源遠流長；中華漢字，寓意深廣．為了傳承中華民族優秀傳統文化，我市某中學舉行“漢字聽寫”比賽，賽后整理參賽學生的成績，將學生的成績分為A，B，C，D四個等級，并將結果繪制成如圖所示的條形統計圖和扇形統計圖，但均不完整．
請你根據統計圖解答下列問題：
（1）參加比賽的學生共有____名；
（2）在扇形統計圖中，m的值為____，表示“D等級”的扇形的圓心角為____度；
（3）組委會決定從本次比賽獲得A等級的學生中，選出2名去參加全市中學生“漢字聽寫”大賽．已知A等級學生中男生有1名，請用列表法或畫樹狀圖法求出所選2名學生恰好是一名男生和一名女生的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，拋物線y＝ax2+bx﹣
與y軸交于點C，與x軸交于點A（﹣1，0），B（3，0）．
（1）求這個拋物線的解析式；
（2）將△AOC以每秒一個單位的速度沿x軸向右平移，平移時間為t秒，平移后的△A′O′C′與△BOC重疊部分的面積為S，A與B重合時停止平移，求S與t的函數關系式；
（3）點P在x軸上，連接CP，點B關于直線CP的對稱點為B′，若點B′落在這個拋物線的對稱軸上，請直接寫出所有符合條件的點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
