
分析 將原式通分整理得$\frac{2(1-2\sqrt{b}+a+b)}{1-2\sqrt{b}+b-a}$=-4,將a+b=1、a=1-b代入整理得$\frac{1}{\sqrt{b}}$=2,即$\sqrt{b}$=$\frac{1}{2}$,根據(jù)a+b=1得出$\sqrt{a}$=$\frac{\sqrt{3}}{2}$,即可得答案.
解答 解:∵$\frac{1-\sqrt{b}+\sqrt{a}}{1-\sqrt{b}-\sqrt{a}}$+$\frac{1-\sqrt{b}-\sqrt{a}}{1-\sqrt{b}+\sqrt{a}}$=-4,
∴$\frac{(1-\sqrt{b}+\sqrt{a})^{2}+(1-\sqrt{b}-\sqrt{a})^{2}}{(1-\sqrt{b})^{2}-(\sqrt{a})^{2}}$=-4,
$\frac{1-2\sqrt{b}+b+2\sqrt{a}(1-\sqrt{b})+a+1-2\sqrt{b}+b-2\sqrt{a}(1-\sqrt{b})+a}{1-2\sqrt{b}+b-a}$=-4,
即$\frac{2(1-2\sqrt{b}+a+b)}{1-2\sqrt{b}+b-a}$=-4,
∵a+b=1,
∴a=1-b,
則$\frac{2(1-2\sqrt{b}+1)}{1-2\sqrt{b}+2b-1}$=-4,
整理得:$\frac{1}{\sqrt{b}}$=2,即$\sqrt{b}$=$\frac{1}{2}$,
∴b=$\frac{1}{4}$,
則a=1-b=$\frac{3}{4}$,
∴$\sqrt{a}$=$\frac{\sqrt{3}}{2}$,
∴$\frac{\sqrt{a}}{\sqrt{b}}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\sqrt{3}$.
點(diǎn)評(píng) 本題主要考查二次根式的化簡(jiǎn)求值,熟練掌握二次根式的混合運(yùn)算順序和法則及整體代入思想是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,直線AB、CD相交于點(diǎn)O,OE平分∠BOD.
如圖,直線AB、CD相交于點(diǎn)O,OE平分∠BOD.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
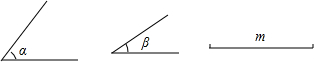
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com