
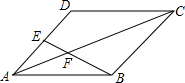
 如圖,在?ABCD中,點E為AD的中點,連接BE,交AC于點F.
如圖,在?ABCD中,點E為AD的中點,連接BE,交AC于點F.分析 (1)根據平行四邊形的性質得出AD=BC,AD∥BC,求出BC=AD=2AE,根據相似三角形的判定得出△AFE∽△CFB即可;
(2)根據相似三角形的性質得出即可;
(3)根據平行線等分線段定理得出AF=FG=CG,即可求出答案.
解答 解:(1)∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC,
∵點E為AD的中點,
∴BC=AD=2AE,
∵AD∥BC,
∴△AFE∽△CFB,
∴$\frac{AF}{CF}$=$\frac{AE}{BC}$=$\frac{1}{2}$;
(2)∵△AFE∽△CFB,$\frac{AF}{CF}$=$\frac{1}{2}$,
∴$\frac{{S}_{△AFE}}{{S}_{BFC}}$=($\frac{AF}{CF}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,
∵S△AEF=9,
∴S△BFC=4×9=36;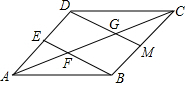
(3)∵E為AD中點,DM∥BE,
∴AF=GF,
∵四邊形ABCD是平行四邊形,
∴AD∥BC,AD=BC,
∵DM∥BE,
∴四邊形DEBM是平行四邊形,
∴BM=DE,
∵E為AD中點,AD=BC,
∴BC=AD=2DE=2AE,
∴MB=CM,
∵DM∥BE,
∴CG=FG,
∴AF=FG=CG,
∵AC=12,
∴FG=4.
點評 本題考查了平行四邊形的性質和判定,相似三角形的性質和判定等知識點,能綜合運用定理進行推理是解此題的關鍵.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:選擇題
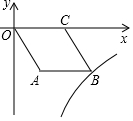 如圖,O是坐標原點,菱形OABC的頂點A的坐標為(6,-8),頂點C在x軸的正半軸上,若函數y=$\frac{k}{x}$(x>0)的圖象經過頂點B,則k的值為( )
如圖,O是坐標原點,菱形OABC的頂點A的坐標為(6,-8),頂點C在x軸的正半軸上,若函數y=$\frac{k}{x}$(x>0)的圖象經過頂點B,則k的值為( )| A. | -48 | B. | -64 | C. | -96 | D. | -128 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m≤3 | B. | m<3 | C. | m<-1 | D. | -1<m<3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| 加油時間 | 加油量(升) | 加油時的累計里程(千米) |
| 2016年2月8日 | 12 | 35000 |
| 2016年2月12日 | 48 | 35600 |
| A. | 6升 | B. | 10升 | C. | 8升 | D. | 12升 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com